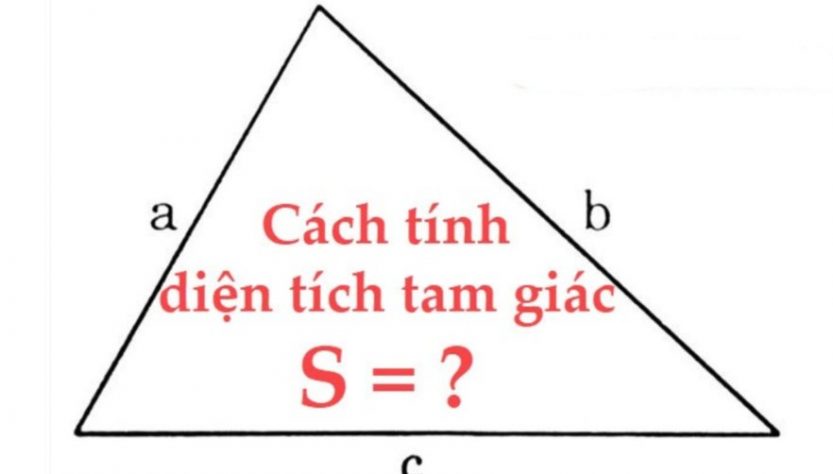
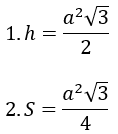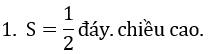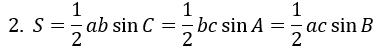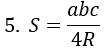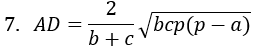Công thức tính diện tích tam giác trong bài toán lớp 5 tưởng chừng như rất đơn giản nhưng nó bao gồm đầy đủ cách tính diện tích tam giác đều, vuông, cân, thường mà các em cần phải nhớ khi áp dụng cho nó vào bài tập. Bài viết dưới đây sẽ hướng dẫn các bạn chi tiết về diện tích tam giác đầy đủ nhất.
Tam Giác Là Gì?
Tam giác là một loại hình cơ bản trong hình học có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau. Tam giác là đa giác đơn và là đa giác có số cạnh ít nhất (3 cạnh). Tổng ba góc trong một tam giác bằng 180 độ. Trong đó có các loại hình tam giác :
+ Tam giác cân: là tam giác có hai cạnh bằng nhau.
+ Tam giác đều: là tam giác có ba cạnh bằng nhau.
+ Tam giác vuông: là tam giác có một góc vuông.
+ Tam giác vuông cân: là tam giác vuông có hai cạnh góc vuông bằng nhau.
Công Thức Tính Diện Tích Tam Giác.
Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao ( cùng một đơn vị đo) rồi chia cho 2.
Ta có công thức : S = (a x h) / 2
Trong đó:
+ a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác tùy theo quy đặt của người tính)
+ h: Chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của một tam giác)
⇒: h= (Sx2)/ A hoặc a= (Sx2)/ h
Bài tập ví dụ:
Tính diện tính tam giác có độ dài đáy là 10 cm, chiều cao 8 cm.
Lời giải
Áp dụng công thức : S = (a x h) / 2
⇒ 10 x 8 : 2 = 40 cm²
Bạn đang xem: Diện Tích Tam Giác
Công thức tính diện tích tam giác vuông
Tam giác vuông là tam giác có một góc bằng 90º (là góc vuông). Trong một tam giác vuông, cạnh đối diện với góc vuông gọi là cạnh huyền, là cạnh lớn nhất trong tam giác đó. Hai cạnh còn lại được gọi là cạnh góc vuông của tam giác vuông
.Công thức tính diện tích tam giác vuông: S = (a x b)/ 2 hoặc S = 1/2 x (a x b)
Bằng chữ : Trong tam giác vuông, nếu coi một cạnh góc vuông là đáy thì cạnh góc vuông còn lại là chiều cao. Diện tích tam giác bằng chiều dài đáy nhân với chiều cao tương ứng rồi chia 2.
Trong đó
+ a: Chiều dài đáy tam giác vuông (đáy là một trong 3 cạnh của tam giác và vuông góc với một cạnh còn lại)
+ a, b: là 2 cạnh góc vuông.
Công Thức Tính Diện Tích Tam Giác Cân
Tam giác cân là tam giác trong đó có hai cạnh bên và hai góc bằng nhau. Trong đó cách tính diện tích tam giác cân cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
Công thức tính diện tích tam giác cân: S = (a x h)/ 2 hoặc S = 1/2 x (a x h)
+ S: là diện tích tam giác cân
+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Công thức tính diện tích tam giác vuông cân
Tam giác vuông cân vừa là tam giác vuông và vừa là tam giác cân. Trong tam giác vuông cân có hai cạnh góc vuông bằng nhau và mỗi góc nhọn bằng 45 độ.
S = 1/2 a²
Trong đó
S : Là diện tích tam giác vuông cân
a : Cạnh của tam giác
Công thức tính diện tích tam giác đều
Hình tam giác đều là tam giác có 3 cạnh bằng nhau, 3 đường cao bằng nhau, 3 đường trung tuyến bằng nhau và 3 đường phân giác bằng nhau hoặc tương đương ba góc bằng nhau và bằng 60º.
S = (a x h)/ 2 hoặc
+ S: là diện tích tam giác điều
+ a: Chiều dài đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
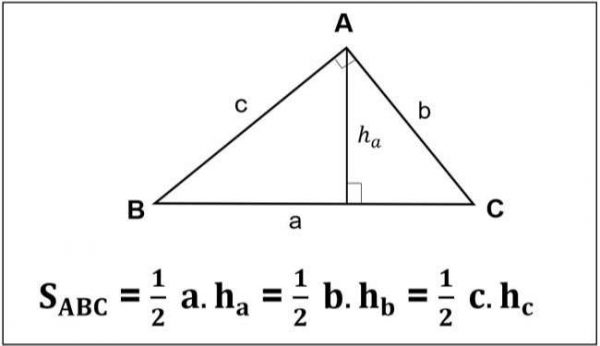
Cách Tính Diện Tích Tam Giác Đầy Đủ
Trong các bài toán tính diện tích tam giác anh chị cần nhớ hết các công thức sau đây để áp dụng vào lời giải bài tập tìm diện tích tam giác khi biết 2 cạnh, 3 cạnh, nửa chu vi…
Với S diện tích, h chiều cao, p=(a+b+c)/2 nửa chu vi, r bán kính nội tiếp, R bán kính ngoại tiếp, trung tuyến AM, phân giác AD.
Trên đây là toàn bộ công thức tính diện tích tam giác mà học sinh cần phải lắm rõ để áp dụng vào cách tính diện tích tam giác vuông, cân, thường, đều có trong trương trình học cũng như các bài kiểm tra xắp đến.