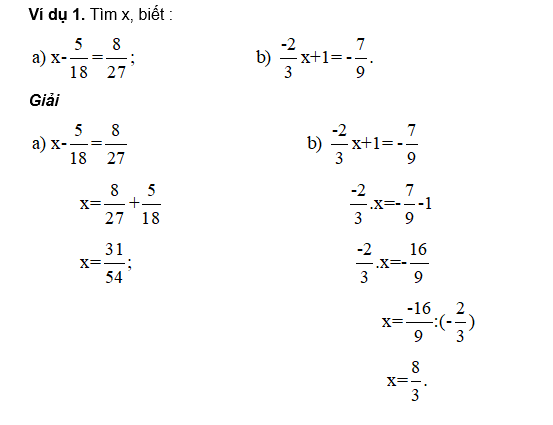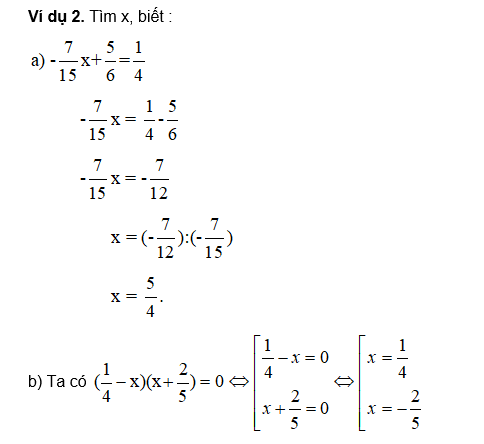Để tìm đại lượng chưa biết trong đẳng thức luỹ thừa, bạn cần sử dụng các phép tính áp dụng trên các bên của đẳng thức để đưa đại lượng chưa biết về một phía và đưa các đại lượng đã biết về phía còn lại. Sau đó, bạn có thể giải phương trình đơn giản để tìm giá trị của đại lượng chưa biết. Mời các bạn tìm hiểu.
Tìm hiểu thêm :
Định nghĩa Lũy Thừa là gì?
Lũy thừa là một phép toán toán học, được viết dưới dạng an, bao gồm hai số, cơ số a và số mũ hoặc lũy thừa n, và được phát âm là “a lũy thừa n”. Khi n là một số nguyên dương, lũy thừa tương ứng với phép nhân lặp của cơ số (thừa số): nghĩa là an là tích của phép nhân n cơ số:
![]()
Số mũ thường được hiển thị dưới dạng chỉ số trên ở bên phải của cơ số. Trong trường hợp đó

Định nghĩa về lũy thừa có thể được mở rộng để cho phép bất kỳ số mũ thực hoặc phức nào. Luỹ thừa theo số mũ nguyên cũng có thể được định nghĩa cho nhiều loại cấu trúc đại số, bao gồm cả ma trận.

Ví dụ
giả sử chúng ta cần tìm giá trị của biến x trong đẳng thức sau đây:
3^x = 81
Để tìm giá trị của x, chúng ta có thể sử dụng phép tính lấy logarit tự nhiên trên cả hai bên của phương trình:
ln(3^x) = ln(81)
Sử dụng tính chất của logarit, chúng ta có thể viết lại phương trình trên thành:
x ln(3) = ln(81)
Sau đó, chúng ta có thể giải phương trình đơn giản này bằng cách chia cả hai bên cho ln(3):
x = ln(81) / ln(3)
Sử dụng máy tính hoặc bảng logarit, chúng ta có thể tính được giá trị chính xác của x, là 4.
Bài tập Vận dụng
Phương pháp giải
– Áp dụng quy tắc bỏ dấu ngoặc, quy tắc “chuyển vế”.
– Vận dụng quan hệ giữa các thừa số với tích của chúng.