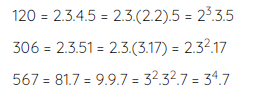Bảng phân tích thừa số nguyên tố là một bảng được sử dụng để phân tích một số nguyên dương thành các thừa số nguyên tố của nó. Bảng này được sắp xếp theo cách tương tự như bảng cửu chương, với các thừa số nguyên tố được sắp xếp theo thứ tự từ nhỏ đến lớn theo hàng ngang và các số nguyên được phân tích được đặt theo hàng dọc. Mời các bạn cùng theo dõi.
Tìm hiểu thêm :
- Hình tứ giác có mấy góc vuông, có bao nhiêu cạnh?
- Xét tính chẵn lẻ của hàm số lượng giác và phương pháp giải.
Phương pháp phân tích một số thành thừa số nguyên tố
Muốn phân tích một số tự nhiên a lớn hơn 1 thành tích của các thừa số nguyên tố ta có thể làm như sau:
- Bước 1: Kiểm tra xem a có chia hết cho 2 hay không? Nếu không, ta tiếp tục xét với số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
- Bước 2: Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương là b.
- Bước 3: Tiếp tục thực hiện phân tích b ra thừa số nguyên tố theo quy trình trên.
- Bước 4: Lặp lại quá trình trên cho đến khi ta được thương là một số nguyên tố.
Phân tích một số ra thừa số nguyên tố theo cột dọc
Giả sử cần phân tích số a ra thành tích của các thừa số nguyên tố. Ta chia số a cho một số nguyên tố (xét lần lượt các số nguyên tố từ nhỏ đến lớn: 2, 3, 5, 7, 11, 13,…), tiếp tục chia thương vừa tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Ví dụ: Phân tích số 40 ra thừa số nguyên tố theo chiều dọc.
Lời giải:
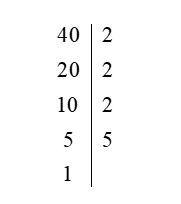
Vậy ta phân tích được: 40 = 2.2.2.5 = 23.5.
Chú ý:
- Mỗi bước phân tích đều lần lượt xét tính chia hết lần lượt cho các số nguyên tố từ nhỏ đến lớn: 2, 3, 5, 7, 11, 13,…
- Vận dụng linh hoạt các dấu hiệu chia hết cho 2, 3, 5, 9 đã học trong quá trình xét tính chia hết.
- Khi phân tích một số ra thừa số nguyên tố theo cột dọc thì các số nguyên tố được viết bên phải cột, các thương được biết bên trái cột.
Phân tích một số ra thừa số nguyên tố theo hàng ngang
Ví dụ: Khi đề bài yêu cầu viết số 40 dưới dạng tích của các thừa số nguyên tố ta làm như sau:
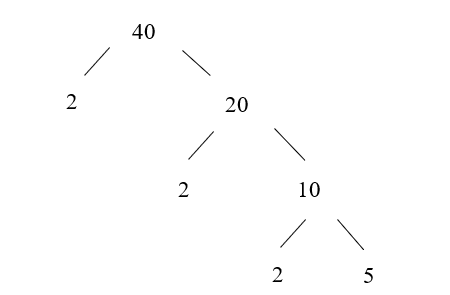
Ta phân tích được: 40 = 2.2.2.5 = 23.5.
Nhận xét: Dù phân tích một số tự nhiên thành tích của các thừa số nguyên tố bằng cách nào thì cũng cho cùng một kết quả.
Ví dụ, bảng phân tích thừa số nguyên tố cho các số từ 1 đến 20 sẽ có dạng như sau:
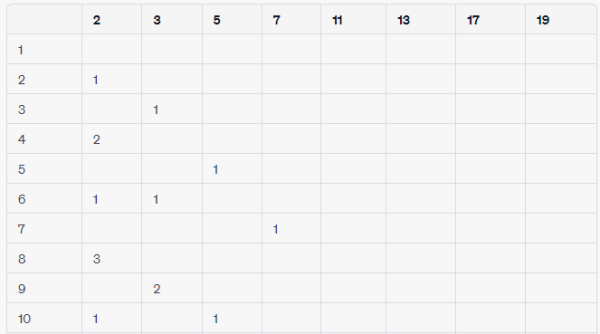
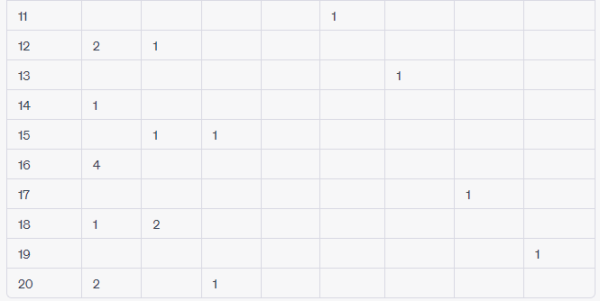
Trong bảng này, ví dụ như số 20 có thể được phân tích thành $2^2\times5$, nên tại hàng số 20 và cột số 2 và cột số 5, ta ghi số 2 và số 5 tương ứng để biểu thị phân tích thừa số nguyên tố của số 20.
Bài tập vận dụng
Bài 1

Bài 2 Phân tích các số sau ra thành tích của các thừa số nguyên tố:

Bài 3 An phân tích các số 120; 306; 567 thành tích các thừa số nguyên tố như sau:
120 = 2.3.4.5
306 = 2.3.51
567 = 9^2.7
An làm như trên có đúng không? Nếu sai hãy sửa lại cho đúng?
Lời giải:
An làm như trên chưa chính xác vì phép phân tích còn chứa các thừa số 4, 51, 9 đều không phải là số nguyên tố. Ta sửa lại như sau (bằng cách tiếp tục phân tích các thừa số không phải số nguyên tố về thành tích của các thừa số nguyên tố).