Công thức đạo hàm là một trong các công thức toán học trong chương trình THPT các bạn cần phải đặc biệt quan tâm. Ở trong bài viết hôm nay chúng ta cùng tìm hiểu bảng công thức đạo hàm cơ bản đến nâng cao đầy đủ nhất để các em có thể tổng quan về bảng đạo hàm dễ dàng nhất.

Công thức đạo hàm là gì?
Công thức đạo hàm là một công thức tính đạo hàm của một hàm số.Với hệ thống bảng công thức đạo hàm từ cơ bản đến nâng cao này sẽ giúp các bạn có thể áp dụng chúng để giải các bài tập một cách nhanh chóng và chính xác nhất.
Công thức đạo hàm cũng là một công cụ quan trọng để giải quyết các bài toán liên quan đến tính toán, xác định điểm cực trị của hàm số, tính tốc độ thay đổi của hàm số và các ứng dụng khác. Với mỗi quy tắc đạo hàm chúng ta sẽ có cách áp dụng riêng cho từng quy tắc.
Đạo hàm là một khái niệm cơ bản trong giải tích toán học, đạo hàm của một hàm số là một đại lượng diễn tả sự biến thiên của hàm tại một điểm nào đó.
Định nghĩa: Đạo hàm của hàm số y=f(x) được ký hiệu là y′(x0) hoặc f′(x0):
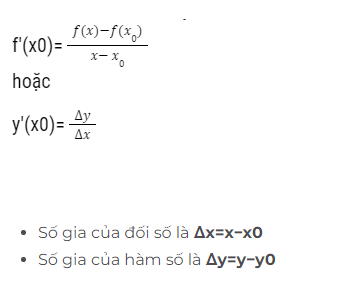
Trong đó:
- Số gia của đối số là x = x – x0.
- Số gia của hàm số là y = y – y0
Bảng công thức đạo hàm từ cơ bản đến cao cấp đầy đủ.
Đối với công thức đạo hàm cơ bản, chúng ta có 3 công thức chính:
- Đạo hàm của f(x) với x là biến số
- Đạo hàm của f(u) với u là một hàm số
- Đạo hàm của một số phân thức hữu tỉ
1. Công thức đạo hàm cơ bản

2. Công thức đạo hàm sơ cấp
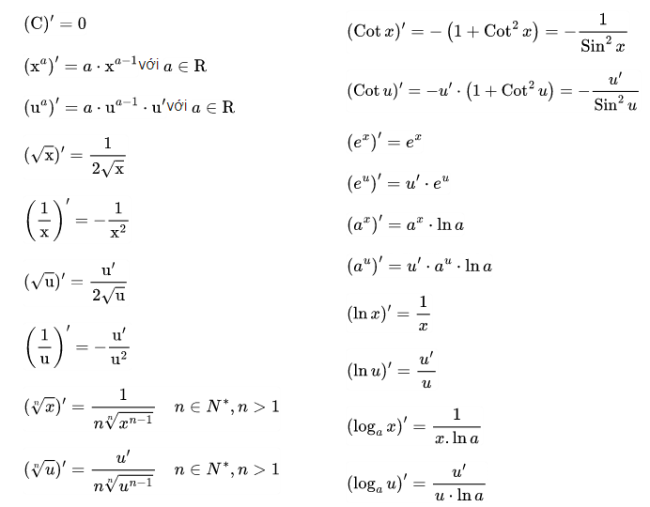
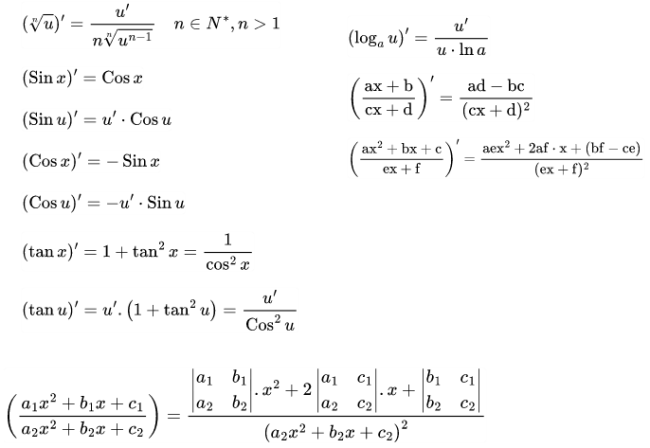
3. Công thức đạo hàm cấp cao
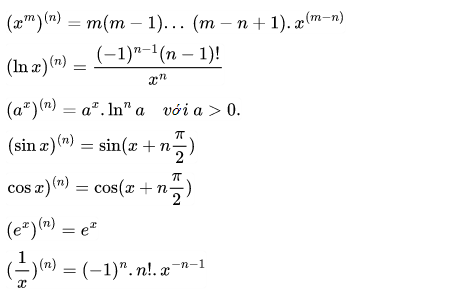
Xem thêm: Công thức hạ bậc
4. Quy tắc cơ bản của đạo hàm
Đối với các quy tắc đạo hàm cơ bản, chúng ta có 2 quy tác đó là:
- Quy tắc cơ bản của tính đạo hàm
- Quy tắc đạo hàm của hàm số hợp

5. Công thức đạo hàm lượng giác
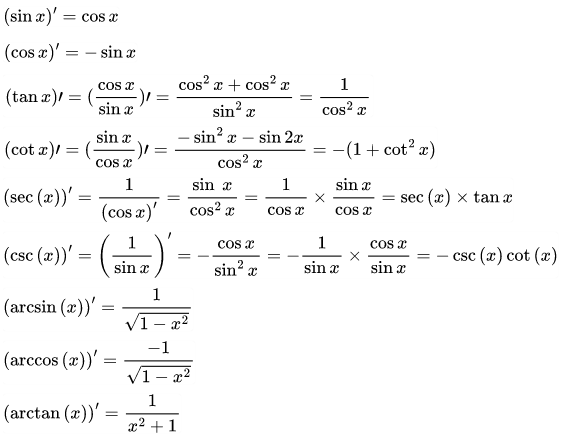
Như vậy trên đây là bảng công thức đạo hàm đầy đủ nhất từ cơ bản đến nâng cao để các bạn nắm rõ các công thức mới giúp bạn có thể giải các bài tập toán về đạo hàm một cách nhanh chóng và chính xác nhất nhé!
Xem thêm: https://svnckh.edu.vn/bang-cac-cong-thuc-luong-giac/
