Tỉ số lượng giác của góc nhọn là kiến thức vô cùng quan trọng đối với học sinh phổ thông, vậy định nghĩa như thế nào là tỉ số lượng giác của góc nhọn, tính chất và phương pháp giải các bài toán liên quan như thế nào cho chính xác nhất.Có những kiến thức nào cần nhớ về tỉ số lượng giác của góc nhọn.
Định nghĩa thế nào là tỉ số lượng giác của một góc nhọn:
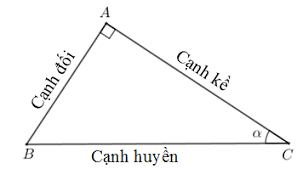
Tỉ số lượng giác của góc nhọn cụ thể là các tỷ số về cạnh của góc nhọn xuất hiện trong các tam giác vuông. Cho tam giác vuông ABC vuông tại A, góc C là góc nhọn được kí hiệu là α.
Ta có: sin α= cạnh đối/ cạnh huyền = AB/BC
cos α= cạnh kề/cạnh huyền = AC/BC
tan α= cạnh đối/cạnh kề = AB/AC
cot α= cạnh kề/cạnh đối = AC/AB
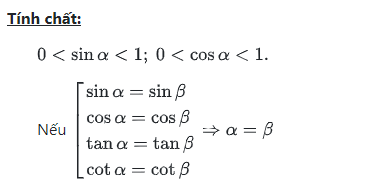

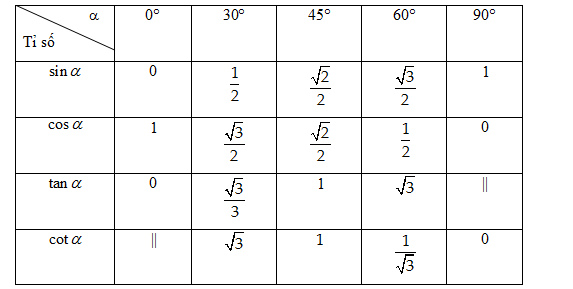
Bảng tỉ số lượng giác của các góc đặc biệt:
Mối liên hệ giữa tỷ số lượng giác của 2 góc nhọn trong tam giác vuông:
Cho tam giác ABC vuông tại A. Góc B và góc C chính là 2 góc nhọn của tam giác vuông và đồng thời phụ nhau. Ta có mối liên hệ giữa tỉ số lượng giác của 2 góc này như sau:


Các dạng toán thường gặp
Dạng 1: Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp:
Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
Dạng 2: So sánh các tỉ số lượng giác giữa các góc
Phương pháp:
Bước 1 : Đưa các tỉ số lượng giác về cùng loại (sử dụng tính chất “Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia”)
Bước 2: Với góc nhọn α,β ta có: sinα<sinβ⇔α<β;cosα<cosβ⇔α>β;
tanα<tanβ⇔α<β;cotα<cotβ⇔α>β.
Dạng 3: Rút gọn, tính giá trị biểu thức lượng giác
Phương pháp:
Ta thường sử dụng các kiến thức
+ Nếu α là một góc nhọn bất kỳ thì
0<sinα<1;0<cosα<1, tanα>0;cotα>0 , sin2α+cos2α=1;tanα.cotα=1
tanα=sinαcosα;cotα=cosαsinα;
1+tan2α=1cos2α;1+cot2α=1sin2α
+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
BÀI TẬP THỰC HÀNH :
Bài 1 : Cho tam giác ABC vuông tại C, AC = 0,9cm, BC = 1,2cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A
Bài làm:
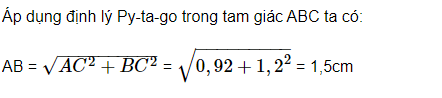

Bài 2: Vẽ một tam giác vuông có một góc nhọn 34 độ rồi viết các tỉ số lượng giác của góc đó.
Hướng dẫn giải:
Đầu tiên ta hãy vẽ một góc vuông B. Trên 1 cạnh góc vuông, ta lấy điểm A.
Sau đó, đặt thước đo độ vào điểm A, đánh dấu góc 34 độ.
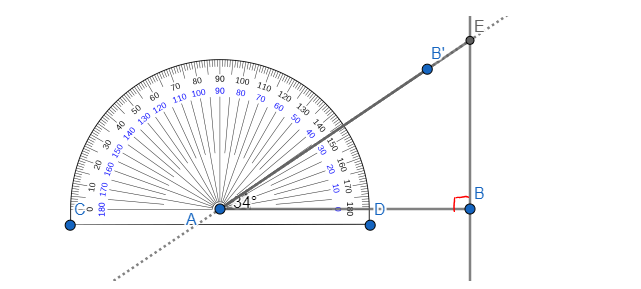
Nối A với điểm ta vừa đánh dấu, kéo dài cắt cạnh góc vuông còn lại tại E.
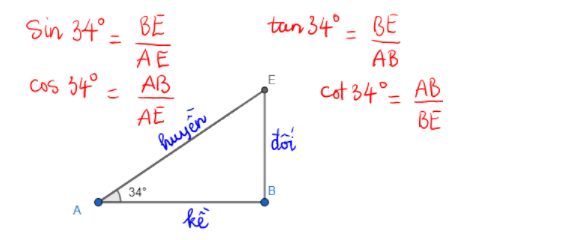
Vậy là ta đã vẽ được hình. Bây giờ các bạn có thể tự viết các tỉ số lượng giác của góc A = 34 độ.
Mời các bạn xem thêm : Hàm số bậc nhất là gì?ý nghĩa và tính chất của hàm số