Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc, để chứng minh và các tính chất của trường hợp này như thế nào? Mời các bạn cùng theo dõi bài viết hôm nay của chúng tôi, kèm bài tập ví dụ có lời giải chi tiết.
Góc Cạnh Góc là gì?
a. Định lý
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
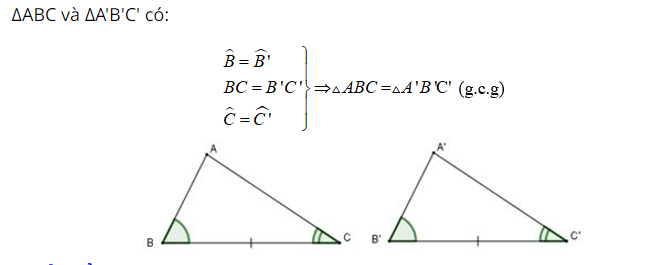
b. Hệ quả:
Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Hệ quả 2. Nếu cạnh huyền và góc nhọn của tam giác vuông nay bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh huyền-góc nhọn)
c. Phương pháp chứng minh 2 tam giác bằng nhau (góc – cạnh – góc)
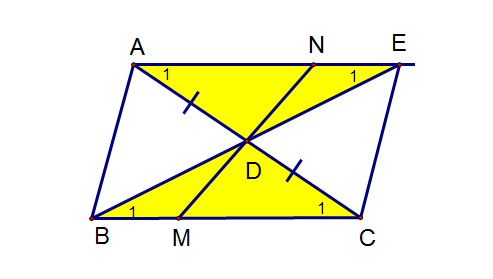
Cho tam giác ABC. Gọi D là trung điểm AC. Từ A vẽ đường thẳng song song BC cắt BD tại E. trên cạnh BC lấy M, đường thẳng DM cắt AE tại N Chứng minh :
- AE = BC.
- D là trung điểm MN.
- AB // EC
Chứng minh
1. AE = BC :
Xét ΔADE và ΔCDB, ta có :
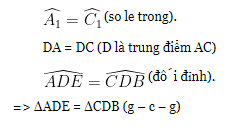
=> AE = BC.
2. D là trung điểm MN :
Xét ΔNDE và ΔMDB, ta có :
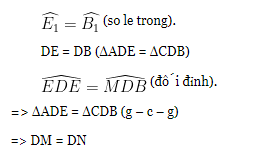
Hay D là trung điểm MN.
3.AB // EC :

=> AB // EC.
d. Bài tập ví dụ
Cho tam giác ABC (AB = AC) và I là trung điểm của đáy BC. Dựng tia Cx song song với tia BA sao cho hai tia BA và Cx nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng BC. Lấy một điểm D nào đó trên AB. Gọi E là một điểm nằm trên tia Cx sao cho BD = CE. Chứng minh rằng ba điểm D, I, E thẳng hàng.
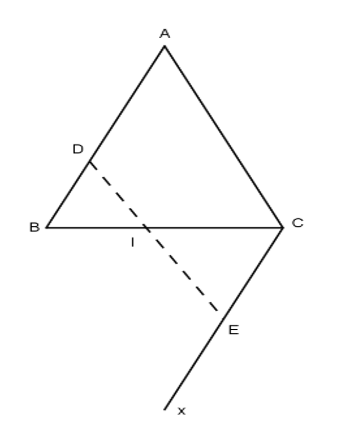
Lời giải
Xét hai tam giác BID và CIE ta có:
BI = IC (I là trung điểm của BC)
∠IBD = ∠ICE (Cx // AB, ∠IBD; ∠ICE hai góc so le trong)
BD = CE (gt)
⇒ ΔBID = ΔCIE (c-g-c)
Nên ∠BID = ∠CIE (hai góc tương ứng bằng nhau)
Hai góc này bằng nhau, chiếm vị trí đối đỉnh, có hai cạnh tương ứng BI và CI nằm trên một đường thẳng.
Như vậy D, I, E thẳng hàng.
Xem thêm: