Hệ thức lượng trong tam giác vuông là kiến thức trong toán lớp lớp 9 mà các bạn cần đặc biệt chú ý! Để tổng hợp lại kiến thức về chuyên đề hệ thức lượng trong tam giác vuông mời các bạn cùng theo dõi ngay ở bài hôm nay, có kèm bài tập hệ thức lượng trong tam giác vuông mà các em cần biết.
Xem thêm: Công thức lượng giác đầy đủ
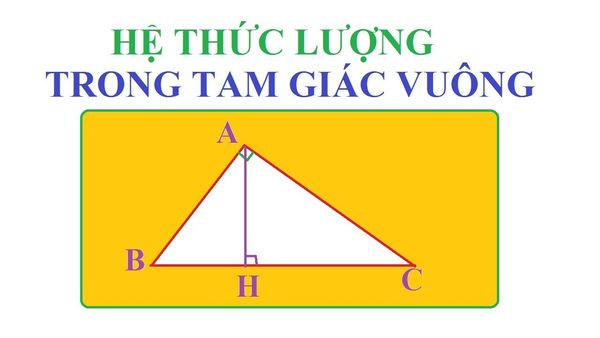
Hệ thức lượng trong tam giác vuông là gì?
1. Hệ thức về cạnh và đường cao trong tam giác vuông
Ta có một hình tam giác vuông ABC vuông tại A và AH là đường cao của tam giác, khi đó ta có các hệ thức cần nhớ liên quan sau đây:
Cho ΔABC, góc A bằng 900, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:
+ BH = c’ được gọi là hình chiếu của AB xuống BC
+ CH = b’ được gọi là hình chiếu của AC xuống BC
Khi đó, ta có:
1) AB2 = BH.BC hay c2 = a.c’
AC2 = CH.BC hay b2 = a.b’
2) AH2 = CH.BH hay h2 = b’.c’
3) AB.AC = AH.BC hay b.c = a.h
5) AB2 + AC2 = BC2 hay b2 + c2 = a2 (Định lý Pytago)
2. Tỉ số lượng giác của góc nhọn
Định lý về tỷ số lượng giác
Trong một tam giác vuông, nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia và ngược lại.
Các hệ thức cơ bản cần nhớ
Ngoài các công thức trên thì để thực hành được các bài tập liên quan một cách tốt nhất. Bạn cũng cần nhớ một số các hệ thức cơ bản dưới đây:/
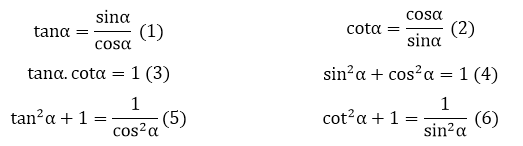
Các so sánh của hệ số lượng giác
Cho 2 góc alpha và belta là 2 góc nhọn của một tam giác vuông và alpha bé hơn belta thì:
a) Cho α,β là hai góc nhọn. Nếu α < β thì
- sinα < sinβ; tanα < tanβ
- cosα > cosβ; cotα > cotβ
b) sinα < tanα; cosα < cotα
3. Các hệ thức lượng trong tam giác vuông về góc và cạnh
a) Trong một tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối, cạnh huyền nhân với cos góc kề. Hay cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề.
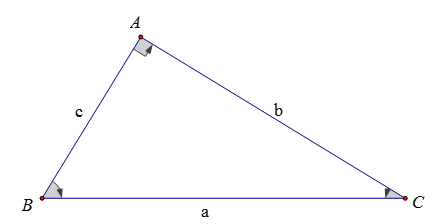
- b = a.sinB = a.cosC
- c = a.sinC = a.cosB
- b = c.tanB = c.cotC
- c = b.tanB = b.cotC
b) Giải một tam giác vuông là tìm tất cả các yếu tố còn lại của một tam giác vuông khi biết trước hai yếu tố. Nhưng phải có ít nhất một yếu tố về cạnh và không kể đến góc vuông.
Định lý lượng giác trong tam giác vuông
Các định lý lượng giác trong tam giác vuông được chúng tôi tổng hợp để các bạn học dinh dễ học và dễ hình dung hơn:
Định lý 1 :Trong một tam giác vuông bất kì, ta luôn có bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền trong tam giác đó và hình chiếu tương ứng của cạnh góc vuông đó ứng với cạnh huyền.
- b² = ab’ ; c² = ac’
Định lý 2 : Trong một tam giác vuông bất kì, bình phương đường cao ứng với cạnh huyền sẽ bằng tích hai hình chiếu của hai cạnh góc vuông tương ứng đó trên cạnh huyền.
- h² = b’c’
Định lý 3 : Trong một tam giác vuông cho sẵn, tích hai cạnh góc vuông bằng tích của cạnh huyền tương ứng và đường cao nối từ đỉnh góc vuông của tam giác đó.
- ah = bc
Định lí 4 : Trong một tam giác vuông được cho sẵn, nghịch đảo của bình phương đường cao ứng với cạnh huyền trong tam giác đó sẽ bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông tương ứng.
Xem thêm: Tính chất hình thang
Bài tập hệ thức lượng trong tam giác vuông.
Bài 1: Cho tam giác CED nhọn, đường cao CH. Gọi M, N theo thứ tự là hình chiếu của H lên CD, CE. Chứng minh:
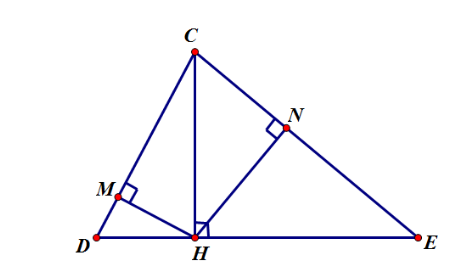
a) CD. CM = CE. CN
b) Tam giác CMN đồng dạng với tam giác CED.
Lời giải
a) Ta cần chứng minh CM.CD = CN. CE
Trước hết, ta cần viết ra CM. CD = ?
Áp dụng hệ thức lượng về cạnh và đường cao:
Trong tam giác vuông CDH : CM.CD = CH²
Trong tam giác vuông CHE: CN.CE = CH²
Như vậy CM. CD = CN.CE (vì cùng = CH²) là điều ta phải chứng minh.
b) Ta cần chứng minh tam giác CMN đồng dạng tam giác CED. Đầu tiên cần tìm xem hai tam giác này có góc chung hay không, có mối liên hệ giữa các cạnh của hai tam giác này không? từ câu a có suy ra được điều gì không?
Ta nhận thấy ngay, hai tam giác CMN và CED có góc C là góc chung.
Như vậy ta có tam giác CMN ∼ CED theo trường hợp Cạnh – Góc – Cạnh.
Bài 2: Cho tam giác ABC vuông tại A có cạnh góc vuông kề với góc 60 độ của tam giác vuông này bằng 3. Sử dụng bảng lượng giác các góc đặc biệt để tìm cạnh huyền và cạnh góc vuông còn lại
Lưu ý: bạn cần phải làm tròn số vừa tính đến chữ số thập phân thứ tư.
Lời giải
Một tam giác ABC vuông cân tại A thì trong 2 góc còn lại, góc lớn hơn là 60 độ và ngược lại là 30 độ. Khi đó cạnh đối diện của góc 60 độ đó bằng 3. Sau đó ta áp dụng từng công thức đã học trong bảng lượng giác để tính cạnh huyền và cạnh góc vuông còn lại.
Chứng minh hình thang? Dấu hiệu nhận biết hình thang, hình thang là gì?