Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”, đây là quy đổi dấu cộng trừ mà học sinh cần nhớ rõ để áp dụng vào bài tập cho chính xác. Để ôn luyện về kiến thức chuyển vế đổi dấu mời các bạn cùng svnckh.edu.vn tìm hiểu ở bài viết hôm nay.

Đổi dấu cộng trừ là gì?
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “-” và dấu “-” đổi thành dấu “+”.
Nếu A + B = C thì A = C – B;
Nếu A – B = C thì A = C + B.
1. Tính chất của đẳng thức
Khi biến đổi các đẳng thức, ta thường áp dụng các tính chất sau:
• Nếu a = b thì a + c = b + c
• Nếu a + c = b + c thì a = b
• Nếu a = b thì b = a
Ví dụ: Tìm số nguyên x, biết: x – 5 = – 8
Giải:
x – 5 = – 8 ⇔ x – 5 + 5 = (- 8) + 5 ⇔ x = -3
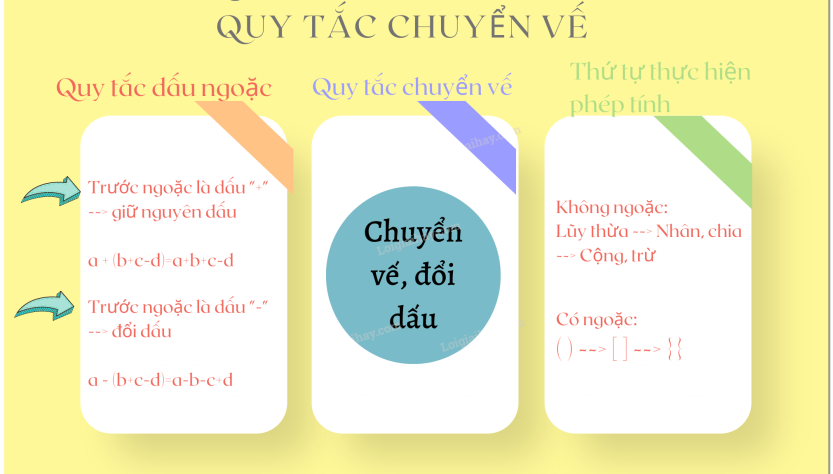
2. Quy tắc chuyển vế
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Ví dụ: Tìm số nguyên x biết x – 2 = – 6
Giải:
x – 2 = – 6 ⇔ x = (- 6) + 2 = – 4
Nhận xét: Ta đã biết a – b = a + (-b) nên (a – b) + b = a + [(-b) + b] = a + 0 = a.
Ngược lại, nếu x + b = a thì sau khi chuyển vế, ta được x = a – b.
Vậy hiệu a – b là số mà khi cộng số đó với b sẽ được a, hay có thể nói phép trừ là phép toán ngược của phép cộng.
Ví dụ:
Ta có:
(9 – 5) + 5 = 9 + [(-5) + 5] = 9 + 0 = 9
(10 – 6) + 6 = 10 + [(-6) + 6] = 10 + 0 = 10
3. Quy tắc dấu ngoặc
Khi bỏ dấu ngoặc
– Đằng trước dấu ngoặc có dấu + thì vẫn giữ nguyên dấu của các số hạng trong dấu ngoặc đó
X + ( y+z-t ) = X + y + z – t
– Nếu đằng trước dấu ngoặc có dấu – thì phải đổi dấu tất cả các số hạng trong ngoặc
X – ( y+z-t ) = X – y -z + t
Bài viết trước: Quy tắc nhân chia trước cộng trừ sau