Nắm vững kiến thức về hình thoi giúp các em giải bài toán cách chứng minh hình thoi đơn giản hơn. Để biết thế nào là hình thoi? Dấu hiệu nhận biết hình thoi như thế nào? Mời các bạn cũng tham khảo trong bài viết hôm nay nhé!
Xem thêm: Dấu hiệu nhận biết hình bình hành

Khái niệm hình thoi là gì?
Hình thoi là tứ giác có bốn cạnh bằng nhau, là hình bình hành đặc biệt với hai cạnh kề bằng và hai đường chéo vuông góc với nhau.
Trong hình thoi:
- Các góc đối nhau bằng nhau
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;
- Hai đường chéo là các đường phân giác của các góc của hình thoi;
- Hình thoi có tất cả tính chất của hình bình hành.
Tính chất của hình thoi
Hình thoi có 4 tính chất như sau:
- Các góc đối nhau bằng nhau.
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc của hình thoi.
- Hình thoi có tất cả tính chất của hình bình hành.
Công thức tính diện tích của hình thoi:
Phát biểu bằng lời: Diện tích hình thoi bằng một nửa tích độ dài của hai đường chéo.
Công thức: S = 1/2 x d1 x d2 = h x a.
Trong đó:
- S: Diện tích hình thoi.
- d1, d2: hai đường chéo hình thoi.
- h: chiều cao của hình thoi.
- a: độ dài cạnh của hình thoi.
Công thức tính chu vi hình thoi
Phát biểu bằng lời: Chu vi của hình thoi được tính bằng tổng độ dài các đường bao quanh hình cũng chính bằng độ dài một cạnh nhân với 4.
Công thức: P = a x 4
Trong đó:
- P là chu vi hình thoi
- a là cạnh hình thoi
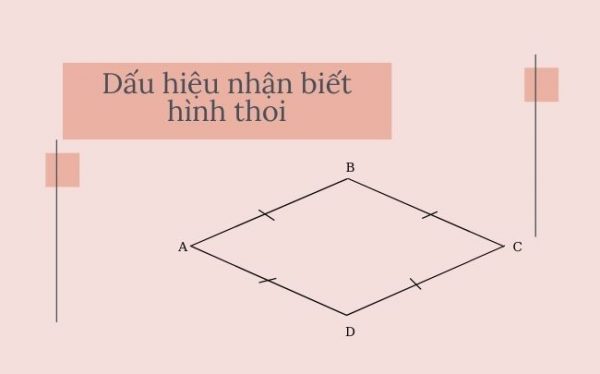
Dấu hiệu nhận biết hình thoi
1. Tứ giác có bốn cạnh bằng nhau là hình thoi.
2. Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.
3. Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
4. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
5. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Cách chứng minh hình thoi
Dựa vào định nghĩa và tính chất, dấu hiệu nhận biết của hình thoi, ta có các cách chứng minh hình thoi như sau:
Cách 1: Chứng minh 4 cạnh của một tứ giác bằng nhau
Ví dụ: Để chứng minh tứ giác MNPQ là một hình thoi thì ta sẽ đi chứng minh:
MN = NP = PQ = QM
Cách 2: Chứng minh một tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường
Ví dụ: Muốn chứng minh tứ giác MNPQ là một hình thoi thì ta sẽ đi chứng minh:
Gọi I là trung điểm của MP và NQ thì: tại I
Cách 3: Chứng minh một tứ giác là hình bình hành có hai cạnh kề bằng nhau
Ví dụ: Nếu MNPQ là hình bình hành thì để chứng minh MNPQ cũng là hình thoi thì ta sẽ đi chứng minh:
MN = NP hoặc NP = PQ hoặc PQ = QM
Cách 4: Chứng minh hình bình hành có một đường chéo là phân giác của một góc
Ví dụ: Nếu MNPQ là hình bình hành thì để chứng minh MNPQ cũng là hình thoi thì ta sẽ đi chứng minh:
NQ là phân giác của góc MNP hoặc góc MQP
MP là phân giác của của góc NPQ hoặc góc NMQ
Cách 5: Chứng minh hình bình hành có hai đường chéo vuông góc với nhau
Ví dụ: Nếu MNPQ là hình bình hành thì để chứng minh MNPQ cũng là hình thoi thì ta sẽ đi chứng minh: MP vuông góc với NQ
Bài tập chứng minh hình thoi
Trong các hình sau, hình nào là hình thoi và chứng minh?
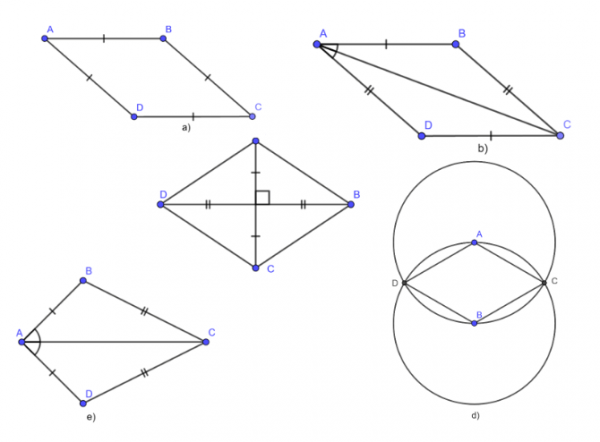
Lời giải
a) Tứ giác ABCD có AB = BC = CD = DA nên ABCD là hình thoi
b) Tứ giác ABCD có AB = CD, AD = BC nên ABCD là hình bình hành.
Hình bình hành ABCD có đường chéo AC là đường phân giác góc Các dấu hiệu nhận biết Hình thoi hay, chi tiết nên ABCD là hình thoi.
c) Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường nên ABCD là hình thoi
d) Ta có: B, C, D đều thuộc đường tròn tâm A nên AB = AC = AD (1)
A, C, D đều thuộc đường tròn tâm B nên AB = BC = BD (2)
Từ (1) và (2) suy ra, AC = AD = BC = BD
⇒ ABCD là hình thoi.
e) Tứ giác ABCD có các cạnh đối diện không bằng nhau, do đó ABCD không là hình thoi.
Như vậy sau kiến thức ngày hôm nay các bạn đã có cách chứng minh hình thoi và các dấu hiệu nhận biết hình thoi đầy đủ nhất khi áp dụng vào giải các bài toán về hình thoi nhé!