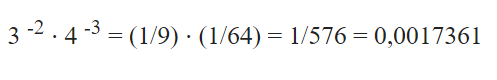Lũy thừa là gì? Công thức cách tính lũy thừa số mũ âm Toán 6

Ở chương trình học THCS chúng ta cùng nhau đi làm quen với các khái niệm về Hàm số lũy thừa là gì? vậy ở bài này chúng ta cùng nhau đi tìm hiểu về Lũy thừa là gì? Công thức cách tính lũy thừa số mũ âm Toán 6. HI vọng sẽ giúp các em củng cố lại kiến thức từ đó có thể vận dụng vào giải quyết các bài tập được dễ dàng và đạt điểm số cao.

Thông tin bài viết mới khác :

Lũy Thừa là gì?

Lũy thừa là một phép toán toán học, được viết dưới dạng an, bao gồm hai số, cơ số a và số mũ hoặc lũy thừa n, và được phát âm là “a lũy thừa n”. Khi n là một số nguyên dương, lũy thừa tương ứng với phép nhân lặp của cơ số (thừa số): nghĩa là an là tích của phép nhân n cơ số:

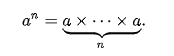
Số mũ thường được hiển thị dưới dạng chỉ số trên ở bên phải của cơ số. Trong trường hợp đó :

Quy tắc số mũ phủ định

– Cơ số b được nâng lên lũy thừa của n thì bằng 1 chia cho cơ số b được nâng lên lũy thừa của n:

Ví dụ về số mũ âm

– Cơ số 2 được nâng lên lũy thừa của trừ 3 bằng 1 chia cho cơ số 2 được nâng lên lũy thừa của 3:

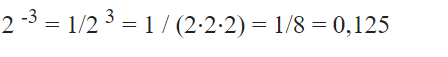
Số mũ phân số âm

– Cơ số b nâng lên lũy thừa của n / m thì bằng 1 chia cho cơ số b nâng lên lũy thừa của n / m:

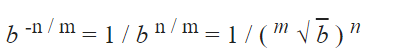
– Cơ số 2 được nâng lên lũy thừa của trừ 1/2 bằng 1 chia cho cơ số 2 được nâng lên lũy thừa của 1/2:

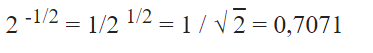
Phân số có số mũ âm

– Cơ số a / b nâng lên lũy thừa của n thì bằng 1 chia cho cơ số a / b nâng lên lũy thừa của n:

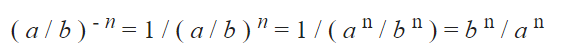
– Cơ số 2 được nâng lên lũy thừa của trừ 3 bằng 1 chia cho cơ số 2 được nâng lên lũy thừa của 3:

Chia số mũ âm

– Đối với các số mũ có cùng cơ số, chúng ta nên trừ các số mũ:

Ví dụ :

– Khi các cơ số khác nhau và số mũ của a và b giống nhau, chúng ta có thể chia a và b trước:

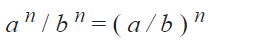
Ví dụ :

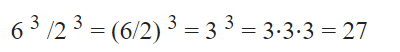
– Khi cơ số và số mũ khác nhau, chúng ta phải tính từng số mũ và sau đó chia:

Ví dụ :

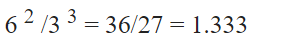
Nhân số mũ âm

– Đối với các số mũ có cùng cơ số, chúng ta có thể thêm các số mũ:

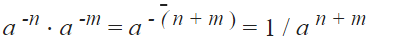
Ví dụ :

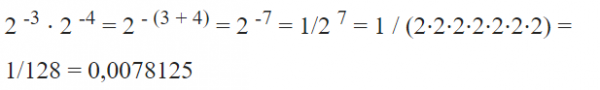
– Khi các cơ số khác nhau và số mũ của a và b giống nhau, chúng ta có thể nhân a và b trước:

Ví dụ :

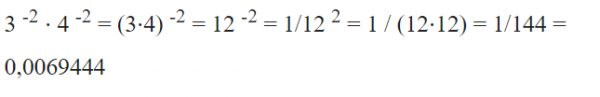
– Khi cơ số và số mũ khác nhau, chúng ta phải tính từng số mũ và sau đó nhân: