Trong các dạng bài tập về hàm số lượng giác, sẽ có các dạng bài toán về xét tính chẵn lẻ của hàm số lượng giác. Như vậy phương pháp giải bài tập dạng này như thế nào? Các bạn cùng theo dõi cách xét tính chẵn lẻ của hàm số lượng giác ngay sau đây.

Xét tính chẵn lẻ của hàm số lượng giác là gì?
Hàm số y = f(x) có tập xác định là D được gọi là hàm số chẵn nếu:
- x ∈ D và – x ∈ D.
- f(x) = f(-x).
Hàm số y = f(x) có tập xác định là D được gọi là hàm số lẻ nếu:
- x ∈ D và – x ∈ D.
- f(x) = – f(-x).
1. Hàm số y=sinx
Tập xác định: R là tập đối xứng.
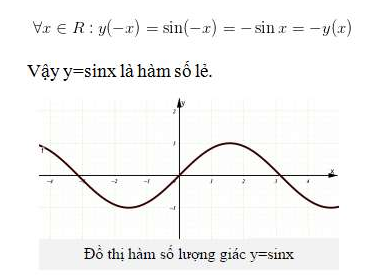
2. Hàm số y=cosx
Tập xác định: R là tập đối xứng.
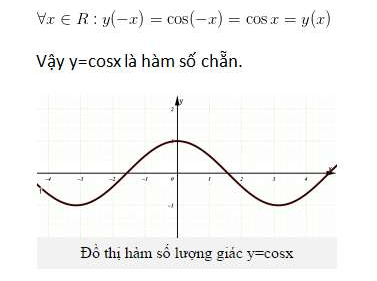
3.Hàm số y = tanx
Tập xác định:
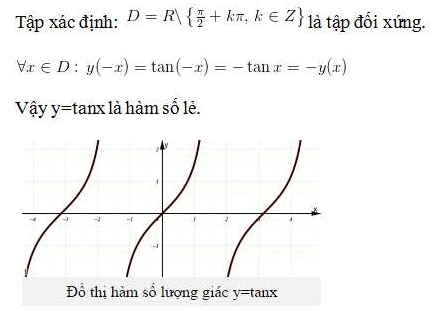
4. Hàm số y=cotx
Tập xác định: D = R\{kπ, k ∈ Z} là tập đối xứng
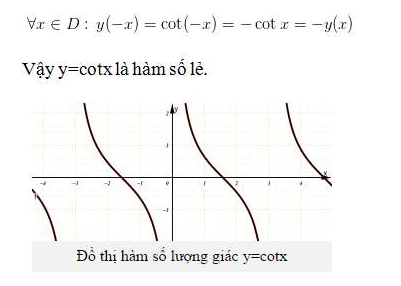
Kết luận: Trong bốn hàm số lượng giác cơ bản duy nhất có hàm số y=cosx là hàm số chẵn. Các hàm số còn lại là hàm số lẻ.
Xem thêm: Cách tìm x trong phép chia có dư
Cách xét tính chẵn lẻ của hàm số lượng giác và bài tập
Bài 1: Xét tính chẵn lẻ của các hàm số sau:
a. y = sinx.
b. y = cos(2x).
Lời giải
a. Tập xác định D = R. Lấy x ∈ D thì – x ∈ D. Ta có: sin (-x) = -sinx. Vậy hàm số đã cho là hàm số lẻ.
b. Tập xác định D = R. Lấy x ∈ D thì – x ∈ D. Ta có: cos(-2x) = cos(2x). Vậy hàm số đã cho là hàm số chẵn.
Bài 2: Xét tính chẵn, lẻ của hàm số
a. y = sinx.cosx
b. y = 1 – cosx
Lời giải
a. Hàm số xác định trên D = R là tập đối xứng (tức ∀x ∈ D ⇒ -x∈D)
Ta có f(-x) = sin(-x).cos(-x) = (-sinx).consx = -sinx.cosx = -f(x)
→Vậy hàm số y = sinx.consx là hàm số lẻ
b. Hàm số xác định trên D = R là tập đối xứng (tức ∀x ∈ D ⇒ -x∈D)
Ta có f(-x) = 1 – cons(-x) = 1 – cosx = f(x)
→ Vậy hàm số y = 1 – cosx là hàm số chẵn.
Bài 3. Hàm số nào sau đây là hàm số chẵn?
A. y= – cosx
B. y= -2sinx
C.y=2sin( -x) .
D y= sinx- cosx
Lời giải:
Chọn A
+ xét phương án A: hàm số y= – 2cosx có tập xác định D= R.
Ta có với x ∈ R ⇒ -x ∈ R v à f(-x)=-2cos(-x)=-2cosx.
⇒ f(x)= f( -x)
Vậy hàm số đã cho là hàm số chẵn.
Bài 4 : Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y= sinx B. y= cosx C. y= tanx D. y= cot x
Lời giải:
Chọn B
+ Hàm số y= sinx là hàm số lẻ.
+ Hàm số y= cosx là hàm số chẵn.
+ Hàm số y= tanx là hàm số lẻ.
+ Hàm số y= cotx là hàm số lẻ.
Vậy B là đáp án đúng.
Bài 5: Xét tính chẵn, lẻ của các hàm số sau:
a) y = cosx + sinx.
b) y = sin2x + cot100x
Lời giải:
a) Ta có tập xác định của hàm số là D = R.
sin (-x) + cos(-x) = – sinx + cosx. Vậy hàm số đã cho là hàm không chẵn, không lẻ.
b) Ta có tập xác định của hàm số là D = R\{k π /100, k ∈ Z}.
sin(-2x) + cot(-100x) = – sin2x – cot(100x). Vậy hàm số đã cho là hàm số lẻ.
Như vậy trên đây là toàn bộ cách xét tính chẵn lẻ của hàm số lượng giác mà các em cần ghi nhớ và bài tập ví dụ có lời giải để các bạn có phương pháp giải bài tập xét tính chẵn lẻ của hàm số lượng giác chuẩn nhất.
Fibonacci là gì? Dãy số, công thức, quy luật Fibonacci trong toán học
