Căn bậc 2 của một số và các tính chất đầy đủ nhất tón học lớp 9

Trong toán học lớp 9 chúng ta sẽ đi tìm hiểu nhiều dạng bài khác nhau, nhưng trước hết phải biết được các ông thức và tính chất của chúng như thế nào thì mới giải được tất cả các bài toán khác nhau. Sau đây chúng ta cùng nhau đi tìm hiểu xem các căn bậc 2 của một số và tính chất của chúng như thế nào nhé. Vậy căn bậc hai của một số là một giá trị mà khi nhân với chính nó sẽ cho ra số ban đầu. Giả sử, x là căn bậc hai của y, khi đó nó được biểu diễn dưới dạng x = √y hoặc chúng ta có thể biểu diễn phương trình tương tự như x 2 = y. Ở đây, ‘√’ là ký hiệu gốc được sử dụng để biểu thị gốc của các số. Số dương, khi nhân với chính nó, đại diện cho bình phương của số . Căn bậc hai của bình phương của một số dương là số ban đầu.

Khái niệm

Căn bậc hai của bất kỳ số nào bằng một số, khi bình phương sẽ cho số ban đầu.
Giả sử m là số nguyên dương, sao cho √ (mm) = √ (m 2 ) = m

Lưu ý: Căn bậc hai của một số âm biểu thị một số phức .

Giả sử √-n = i√n, với i là số ảo.

Công thức :

Công thức để tìm căn bậc hai là:

y = √a
Vì, yy = y 2 = a; trong đó ‘a’ là bình phương của một số ‘y’.

Lý thuyết về hệ số góc của đường thẳng y=ax+b (a # 0)

Tính chất :

Trong toán học, hàm căn bậc hai được định nghĩa là hàm một đối một lấy một số dương làm đầu vào và trả về căn bậc hai của số đầu vào đã cho.

f (x) = √x

Ví dụ: nếu x = 9, thì hàm trả về giá trị đầu ra là 3. Một số thuộc tính quan trọng của căn bậc hai như sau:

Nếu một số là một số bình phương hoàn hảo, thì tồn tại một căn bậc hai hoàn hảo.
Nếu một số kết thúc bằng số chẵn (0) thì nó có thể có căn bậc hai.
Hai giá trị căn bậc hai có thể được nhân lên. Ví dụ, √3 có thể nhân với √2, thì kết quả sẽ là √6.
Khi hai căn bậc hai giống nhau được nhân lên, thì kết quả sẽ là một số căn. Nó có nghĩa là kết quả là một số không căn bậc hai. Ví dụ, khi √7 nhân với √7, kết quả nhận được là 7.
Căn bậc hai của bất kỳ số âm nào không được xác định. Bởi vì hình vuông hoàn hảo không thể là âm.
Nếu một số kết thúc bằng 2, 3, 7 hoặc 8 (ở hàng đơn vị), thì căn bậc hai hoàn hảo không tồn tại.
Nếu một số kết thúc bằng 1, 4, 5, 6 hoặc 9 ở chữ số hàng đơn vị, thì số đó sẽ có căn bậc hai.

Các cách tìm căn bậc 2 :

Để tìm căn bậc hai của bất kỳ số nào, chúng ta cần tìm xem số đã cho là một bình phương hoàn hảo hay bình phương không hoàn hảo. Nếu số là một hình vuông hoàn hảo, chẳng hạn như 4, 9, 16, v.v., thì chúng ta có thể phân tích số bằng phương pháp thừa số nguyên tố. Nếu số là một bình phương không hoàn hảo, chẳng hạn như 2, 3, 5, v.v., thì chúng ta phải sử dụng phương pháp chia dài để tìm căn.
Ví dụ: Bình phương của 7 = 7 x 7 = 7 2 = 49
Căn bậc hai của 49, √ 49 = 7

Căn bậc hai theo thừa số nguyên tố
Căn bậc hai của một số bình phương hoàn hảo rất dễ tính bằng phương pháp phân tích thừa số nguyên tố.

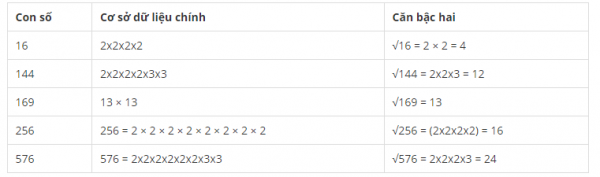
Cách tìm căn bậc hai bằng phương pháp chia
Tìm căn bậc hai cho các số không hoàn hảo là một chút khó khăn nhưng chúng ta có thể tính toán bằng cách sử dụng một phương pháp chia dài. Điều này có thể được hiểu với sự trợ giúp của ví dụ dưới đây. Hãy xem xét một ví dụ về việc tìm căn bậc hai của 436.

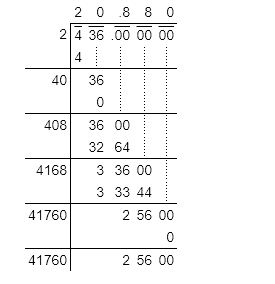
Như vậy, căn bậc hai của 436 là 20,880 (làm tròn đến 3 số thập phân).

Căn bậc 2 của số thập phân :

Một giá trị thập phân sẽ có dấu chấm (.) Chẳng hạn như 3,8, 5,2, 6,33, v.v. Đối với một số nguyên, chúng ta đã hiểu cách lấy căn bậc hai nhưng chúng ta hãy xem cách lấy căn bậc hai của một số thập phân.

Ví dụ: Tìm căn bậc hai của 0,09.
Cho N 2 = 0,09
Lấy gốc ở cả hai phía.
N = ± √0,09
Như chúng ta đã biết,
0,3 x 0,3 = (0,3) 2 = 0,09
Do đó,
N = ± √ (0,3) 2
N = ± (0,3)

Căn bậc 2 của số phức :

Để tìm căn bậc hai của số phức hơi phức tạp. Chúng ta có thể tìm căn bậc hai của a + ib bằng công thức dưới đây:

a + b i—–√= ± (a2+b2+ a√2——-√+ tôia2+b2– một√2——-√)
trong đó a + ib là một số phức.

Cách giải phương trình căn bậc 2 :

Một phương trình căn bậc hai là một phương trình có một biến trong bán kính của căn. Nó còn được gọi là phương trình căn.

Để giải phương trình căn, chúng ta cần làm theo các bước sau:

Cô lập căn bậc hai cho một trong các cạnh (LHS hoặc RHS).
Bình phương cả hai vế của phương trình đã cho
Bây giờ giải phương trình còn lại.

Bình phương và căn bậc 2 từ 1 đến 10 :

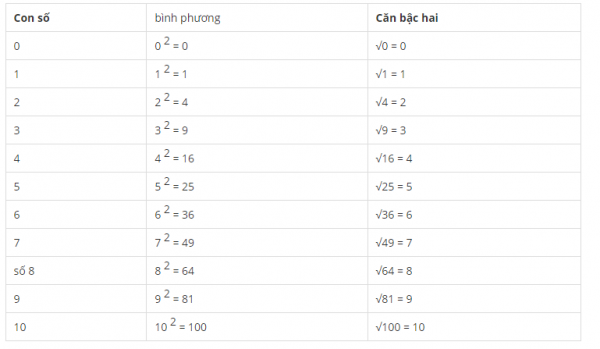
Bài tập ứng dụng :

Ví dụ: Giải phương trình nghiệm nguyên √ (4a + 9) – 5 = 0
Giải: Cho, √ (4a + 9) – 5 = 0

Cô lập số hạng căn bậc hai đầu tiên. Sau đó, phương trình trở thành,

√ (4a + 9) = 5

Bây giờ bình phương cả hai bên, chúng ta nhận được; 4a + 9 = 5 2
4a + 9 = 25

4a = 16

a = 16/4

a = 4

Điều kiện 1: Nếu phương trình có nhiều hơn một căn hoặc căn bậc hai.
Nếu phương trình căn có nhiều hơn một căn thì lặp lại các bước đã cho ở trên cho mỗi căn bậc hai.

Ví dụ: Giải √ (2x − 5) – √ (x − 1) = 1

Hãy để chúng tôi tách một trong những căn bậc hai.

√ (2x − 5) = 1 + √ (x − 1)

Bây giờ bình phương cả hai bên

2x – 5 = (1 + √ (x − 1)) 2

Áp dụng đồng nhất đại số, (a + b) 2 = a 2 + b 2 + 2ab.

2x − 5 = 1 + 2√ (x − 1) + (x − 1)

2x − 5 = 2√ (x − 1) + x

x − 5 = 2√ (x − 1)

Bây giờ một lần nữa cô lập căn bậc hai.

√ (x − 1) = (x − 5) / 2

x − 1 = ((x − 5) / 2) 2