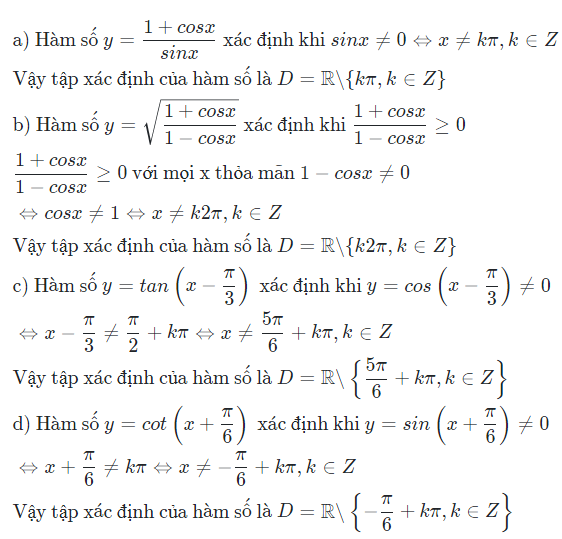Công thức hàm số lượng giác 11 là kiến thức rất quan trọng với học sinh Thpt, ở bài viết hôm nay hãy cùng https://svnckh.edu.vn/ tìm hiểu Hàm số lượng giác là gì? và bài tập hàm số lượng giác chi tiết mời các bạn cùng theo dõi.
Hàm số lượng giác là gì?
Hàm số lượng giác là một loại hàm số trong toán học, được sử dụng để tính toán giá trị của các hàm lượng giác của các góc trong tam giác vuông. Các hàm lượng giác phổ biến nhất bao gồm sin, cos và tan, và chúng được định nghĩa là các tỉ số của các cạnh của tam giác vuông tương ứng với góc trong tam giác đó.
Cụ thể, sin của một góc trong tam giác vuông là tỉ số giữa cạnh đối diện với góc đó và độ dài của đường chéo (hay đường cao) đi qua góc đó, cos của một góc trong tam giác vuông là tỉ số giữa cạnh kề với góc đó và độ dài của đường chéo (hay đường cao) đi qua góc đó, và tan của một góc trong tam giác vuông là tỉ số giữa cạnh đối diện với góc đó và cạnh kề với góc đó.
Hàm số lượng giác được sử dụng rộng rãi trong các lĩnh vực như toán học, vật lý, kỹ thuật và khoa học máy tính.
Xem thêm: Fibonacci là gì?
Các công thức hàm số lượng giác 11

Công thức hàm số lượng giác cơ bản
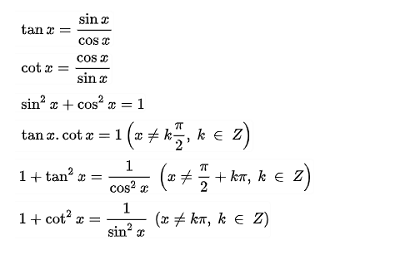
Công thức hàm số lượng giác trong trường hợp đặc biệt:
sin a = 0 ⇔ a = kπ; (k ∈ Z)
sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)
sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)
cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)
cos a = 1 ⇔ a = k2π; (k ∈ Z)
cos a = -1 ⇔ a = π + k2π; (k ∈ Z)
Xem thêm: Các phép tính cộng trừ có nhớ lớp 2 trong phạm vi 10, 20, 100
Công thức cộng trong hàm số lượng giác
1. sin (a ± b) = sin a.cos b ± cos a.sin b
2. cos (a + b) = cos a.cos b – sin a.sin b
3. cos (a – b) = cos a.cos b + sin a.sin b
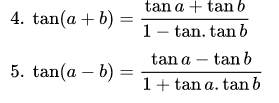
Công thức các cung liên quan trên đường tròn lượng giác
1. Hai góc đối nhau:
cos (-x) = cos x
sin (-x) = -sin x
tan (-x) = -tan x
cot (-x) = -cot x
2. Hai góc bù nhau:
sin (π – x) = sin x
cos (π – x) = -cos x
tan (π – x) = -tan x
cot (π – x) = -cot x
3. Hai góc phụ nhau:
sin (π/2 – x) = cos x
cos (π/2 – x) = sin x
tan (π/2 – x) = cot x
cot (π/2 – x) = tan x
4. Hai góc hơn kém π:
sin (π + x) = -sin x
cos (π + x) = -cos x
tan (π + x) = tan x
cot (π + x) = cot x
5. Hai góc hơn kém π/2:
sin (π/2 + x) = cos x
cos (π/2 + x) = -sin x
tan (π/2 + x) = -cot x
cot (π/2 + x) = -tan
Công thức nhân
1. Công thức nhân đôi
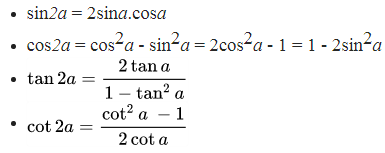
2. Công thức nhân 3.
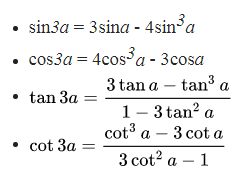
3. Công thức nhân bốn
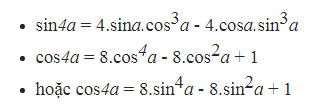
4. Công thức hạ bậc
Xem chi tiết: Công thức hạ bậc
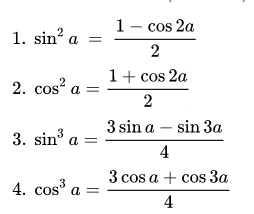
Công thức biến tổng thành tích
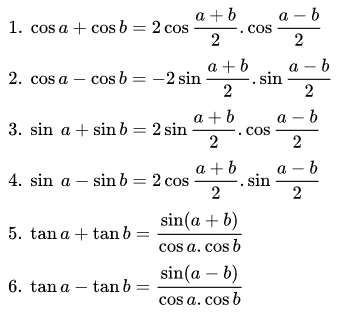
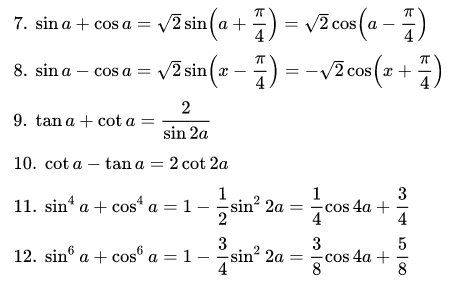
Công thức biến đổi tích thành tổng
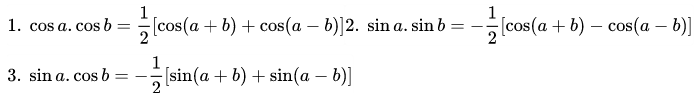
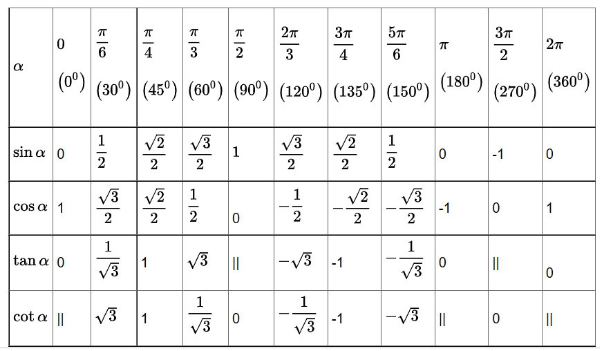
Dấu của các giá trị lượng giác

Bảng giá trị lượng giác một số góc đặc biệt
Công thức lượng giác bổ sung
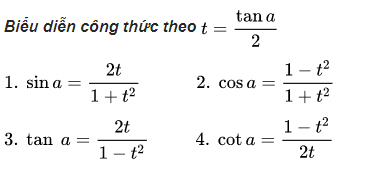
Xem chi tiết: Bảng các công tức lượng giác
Bài tập hàm số lượng giác 11
Tìm tập xác định của các hàm số sau
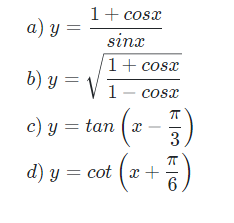
Lời giải