Toán lớp 6 lũy thừa với số mũ tự nhiên là kiến thức mà các em cần nắm rõ trong chương trình học. Để ôn tập về giải bài tập, cùng lý thuyết lũy thừa với số mũ tự nhiên là gì? Mời các bạn cùng theo dõi chi tiết trong bài học ngày hôm nay.
Lũy thừa với số mũ tự nhiên là gì?
1. Định nghĩa lũy thừa với số mũ tự nhiên
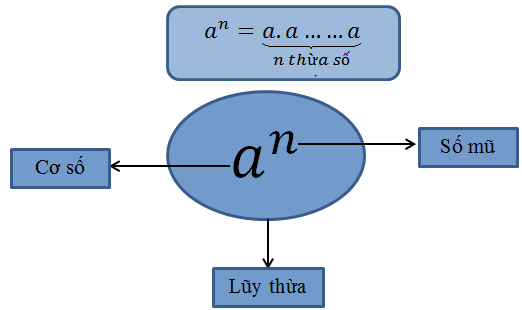
Lũy thừa bậc n của a, kí hiệu là a^n, là tích của n thừa số a: a^n = a.a.a…a (n thừa số a) với n là số tự nhiên.
Số a được gọi là cơ số, n được gọi là số mũ.
Ta quy ước: a^1 = a; 1^n = 1; a^0 = 1
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.
- a^n đọc là “a mũ n” hoặc “a lũy thừa n” hoặc “lũy thừa bận n của a”
- a^2 còn được gọi là “a bình phương” hay “bình phương của a”.
- a^3 còn được gọi là “a lập phương” hay “lập phương của a”.
- 0^n không có nghĩa.
Với n là số tự nhiên khác 0, ta có: 10^n = 100….0 (n chữ số 0)
Xem thêm: Số chẵn là gì
2. Tính chất của lũy thừa với số mũ tự nhiên
– Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: a^m.a^n = a^m+n
– Khi chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và trừ các số mũ: a^m : a^n = a^m-n (a khác 0, m >= n)
Mở rộng:
(a.b)^n = (a.b).(a.b)….(a.b) (gồm n thừa số a.b) = a^n. b^n
(a : b)^n = (a. a. a… a) : (b. b.b… b) (gồm n thừa số a, n thừa số b) = a^n : b^n (b khác 0)
(a^n)^m = a^n. a^n. a^n… a^n (gồm m thừa số a^n) = a^n.m.
3. Nhân hai lũy thừa cùng cơ số
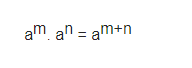
Khi nhân hai lũy thừa cùng cơ số, ta giữa nguyên cơ số và cộng các số mũ.
4. Chia hai lũy thừa cùng cơ số
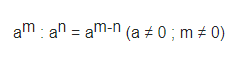
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
5. Lũy thừa của lũy thừa
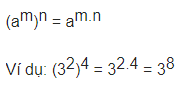
6. Nhân hai lũy thừa cùng số mũ, khác sơ số
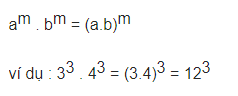
7. Chia hai lũy thừa cùng số mũ, khác cơ số
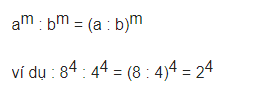
Xem thêm: Kết quả phép chia gọi là gì?
8. Quy ước
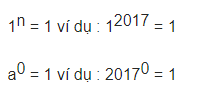
Phương pháp giải bài tập lũy thừa với số mũ tự nhiên
Dạng 1: Viết kết quả phép tính nhân, chia dưới dạng lũy thừa
Cách giải: Để viết kết quả phép tính dưới dạng lũy thừa, ta biến đổi phép tính về dạng phép nhân các lũy thừa cùng cơ số hoặc phép chia hai lũy thừa cùng cơ số, rồi áp dụng quy tắc nhân các lũy thừa cùng cơ số hoặc chia hai lũy thừa cùng cơ số để viết gọn kết quả.
Dạng 2: So sánh các số viết dưới dạng lũy thừa. Tìm số mũ của lũy thừa
Cách giải : Để so sánh các số viết dưới dạng lũy thừa, ta có thể làm theo 3 cách sau đây:
Cách 1: Đưa lũy thừa về cùng cơ số là số tự nhiên rồi so sánh hai số mũ
Nếu m > n thì a^m > a^n
Cách 2: Đưa lũy thừa về cùng số mũ rồi so sánh hai cơ số
Nếu a > b thì a^m > b^m
Cách 3: Tính cụ thể từng lũy thừa rồi so sánh
Dạng 3: Tim chữ số tận cùng của một số dạng lũy thừa
Cách giải: Dựa vào các tính chất sau đây để tìm chữ số tận cùng của một số dạng lũy thừa
– Một số chính phương (là bình phương của một số tự nhiên) có tận cùng là 0, 1, 4, 5, 6, 9
– Một số nguyên tố lớn hơn 5 chỉ có thể tận cùng bằng 1, 3, 7, 9
– Chữ số tận cùng của a^n chính là chữ số tận cùng của x^n (với x là chữ số tận cùng của a)
– Các số có chữ số tận cùng là 0, 1, 5, 6 khi nâng lên lũy thừa bậc bất kỳ thì chữ số tận cùng vẫn không thay đổi
– Các số có chữ số tận cùng là 4, 9 khi nâng lên lũy thừa bậc lẻ thì chữ số tận cùng vẫn không thay đổi
– Các số có chữ số tận cùng là 3, 7, 9 khi nâng lên lũy thừa bậc 4n (n là số tự nhiên) thì chữ số tận cùng là 1
– Các số có chữ số tận cùng là 2, 4, 8 khi nâng lên lũy thừa bậc 4n (n là số tự nhiên) thì chữ số tận cùng là 6.
– Một số tự nhiên bất kì khi nâng lên lũy thừa bậc 4n + 1 (n là số tự nhiên) thì chữ số tận cùng vẫn không thay đổi
– Số tự nhiên có chữ số tận cùng là 3 khi nâng lên lũy thừa bậc 4n + 3 sẽ có chữ số tận cùng là 7; số tự nhiên có chữ số tận cùng là 7 khi nâng lên lũy thừa bậc 4n + 3 sẽ có chữ số tận cùng là 3
– Số tự nhiên có chữ số tận cùng là 2 khi nâng lên lũy thừa bậc 4n + 3 sẽ có chữ số tận cùng là 8; số tự nhiên có chữ số tận cùng là 8 khi nâng lên lũy thừa bậc 4n + 3 sẽ có chữ số tận cùng là 2
– Các số tự nhiên có chữ số tận cùng là 0, 1, 4, 5, 6, 9 khi nâng lên lũy thừa bậc 4n + 3 sẽ không thay đổi chữ số tận cùng.
– Chữ số tận cùng của một tổng các lũy thừa được xác định bằng cách tính tổng các chữ số tận cùng của từng lũy thừa trong tổng.
Như vậy trên đây là toàn bộ kiến thức lũy thừa với số mũ tự nhiên toán lớp 6, kèm lời giải các dạng bài tập liên quan đến lũy thừa với số mũ tự nhiên mà các em cần nắm được nhé!
Lũy thừa của một số hữu tỉ toán lớp 7 “Công thức và cách giải bài tập”.