Hình vuông khá quen thuộc với chúng ta trong cuộc sống hàng ngày, nhưng có thể bạn chưa biết tính chất hình vuông và khái niệm hình vuông là gì? Trong bài viết hôm nay chúng ta cùng tìm hiểu tính chất của hình vuông nhé!
Khái niệm hình vuông là gì?
Hình vuông là tứ giác có bốn góc vuông và có 4 cạnh bằng nhau.
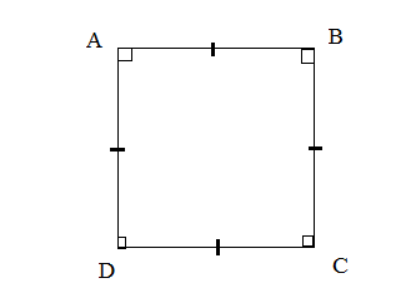
Xét tứ giác ABCD là hình vuông ⇔ góc A = góc B = góc C = góc D = 90°
Và AB = BC = CD = DA
Từ đây ta nhận thấy rằng:
- Hình vuông là hình chữ nhật có bốn cạnh bằng nhau
- Hình vuông là hình thoi có bốn góc vuông
Suy ra: Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
Tính chất của hình vuông
Hình vuông có đầy đủ những tính chất sau đây:
- Hai đường chéo hình vuông bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
- Giao điểm hai đường chéo của hình vuông là tâm của đường tròn nội tiếp và ngoại tiếp.
- Có một đường tròn nội tiếp và ngoại tiếp, đồng thời tâm của cả hai đường tròn trùng nhau và là giao điểm của hai đường chéo của hình vuông.
- Giao của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.
- Một đường chéo sẽ chia hình vuông thành hai phần có diện tích bằng nhau.
- Hình vuông có tất cả tính chất của hình chữ nhật và hình thoi.
Xem thêm:
Bài tập chứng minh hình vuông
Bài 1: Cho hình sau đây, hỏi tứ giác AEDF là hình gì? Vì sao?
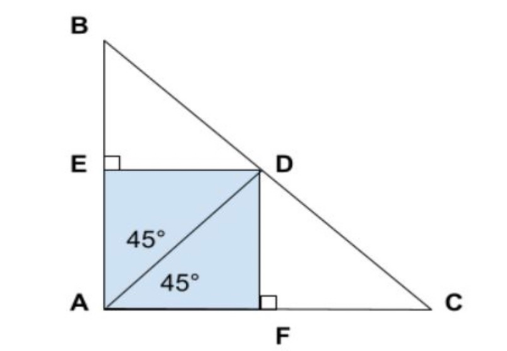
Lời giải
Ta có: EA⊥AF, DF⊥AF ( như hình vẽ)
⇔ EA // DF (tính chất song song)
Ta có: DE⊥AB, AF⊥AB (hình vẽ)
⇔ DE // AF (tính chất song song)
Xét tứ giác AEDF có EA // DF, DE // AF (cmt)
⇔ Tứ giác AEDF là hình bình hành (định nghĩa)
Xét hình bình hành AEDF có đường chéo AD là phân giác của góc A (∠EAD = ∠DAF = 45°)
⇒ Tứ giác AEDF là hình thoi.
Xét hình thoi AEDF có ∠BAC = ∠EAD + ∠DAF = 45°+45° = 90º
⇒ Tứ giác AEDF là hình vuông.
Bài 2. Cho hình bên, tứ giác AEDF là hình gì? Chứng minh?

Lời giải
Tứ giác AEDF là hình vuông, vì:
Theo hình vẽ, góc A = góc E = góc F = 90°
Tứ giác có ba góc vuông nên nó là hình chữ nhật (DHNB).
Xét hình chữ nhật AEDF có AD là đường phân giác của góc A (góc FAE = góc EAD = 45°)
⇒ AEDF là hình vuông
Bài 3: Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.
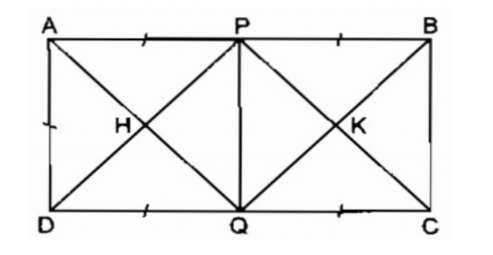
Lời giải
Xét tứ giác APQD, ta có: AB // CD (gt) hay AP // QD
AP = AB (gt)
QD = 1/2 CD (gt)
Suy ra: AP = QD
Hay tứ giác APQD là hình bình hành.
Lại có: ∠A = 90º
Suy ra tứ giác APQD là hình chữ nhật.
Mà AD = AP = 1/2 AB
Vậy tứ giác APQD là hình vuông.
⇒ AQ ⊥ PD (tính chất hình vuông) ⇒ ∠(PHQ) = 90º (1)
HP = HQ (tính chất hình vuông)
* Xét tứ giác PBCQ, ta có: PB // CD
PB = 1/2 AB (gt)
CQ = 1/2 CD (gt)
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
∠B = 90º suy ra tứ giác PBCQ là hình chữ nhật
PB = BC (vì cùng bằng AD = 1/2 AB)
Vậy tứ giác PBCQ là hình vuông
⇒ PC ⊥ BC (tính chất hình vuông) ⇒ ∠(PKQ) = 90º (2)
PD là tia phân giác ∠(APQ) (tính chất hình vuông)
PC là tia phân giác ∠(QPB) (tính chất hình vuông)
Suy ra: PD ⊥ PC (tính chất hai góc kề bù) ⇒ ∠(HPK) = 90º (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.
Trên đây là toàn bộ khái niệm hình vuông và tính chất hình vuông mà chúng tôi muốn gửi đến các bạn khi áp dụng vào bài tập chứng minh hình vuông đơn gản hơn.