Trong dạng toán đồ thị hàm số có một chủ đề mới khá đặc sắc, mới lạ với toán lớp 9. Đó là khái niệm về tiếp tuyến vậy tiếp tuyến là gì? những dấu hiệu nhận biết tiếp tuyến đường tròn? các cách giải bài tập như thế nào, xin mời các em tìm hiểu ở bài viết dưới đây để biết được cách nhận biết tiếp tuyến của đường tròn.
Định nghĩa:
Tiếp tuyến là đường thẳng chỉ tiếp xúc đường tròn tại một điểm, đồng thời nó cũng vuông góc với bán kính của đường tròn tại điểm đó.
Một số dấu hiệu cần ghi nhớ như sau:
Nếu có một đường thẳng đồng thời qua một điểm trên đường tròn và vuông góc với bán kính thì đường thẳng đó là tiếp tuyến.
Nếu một đường thẳng và đường tròn chỉ có một điểm chung thì đường thẳng đó là tiếp tuyến của đường tròn
Nếu khoảng cách từ tâm của đường tròn đến đường thẳng đã cho đúng bằng bán kính. Vậy đường thẳng đó là tiếp tuyến của đường tròn.
Tính chất tiếp tuyến của đường tròn :
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm
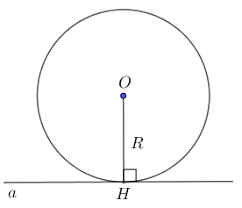
Trong hình trên a là tiếp tuyến của đường tròn (O) .⇒a ⊥ OH tại H (với H là tiếp điểm).
Bảng lượng giác là gì? Cấu tạo của bảng lượng giác
Các hình thức về cạnh và đường cao trong tam giác vuông
Đường thẳng song song và đường thẳng cắt nhau
Dấu hiệu nhận biết tiếp tuyến của đường tròn
Định lý : Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
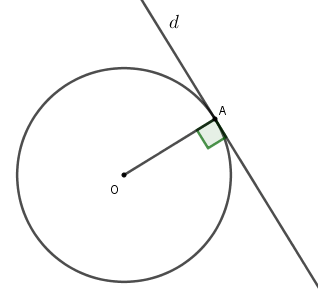
Ngoài ra, nhắc lại một số dấu hiệu đã biết:
+) Nếu một đường thằng và một đường tròn chỉ có một điểm chung thì đường thẳng đó là tiếp tuyến của đường tròn.
+) Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
Các dạng toán thường gặp

Bài tập vận dụng :
Câu 1 :
Cho tam giác ABC, đường cao AH. Chứng minh rằng đường thẳng BC là tiếp tuyến của đường tròn (A; AH).
Lời giải :
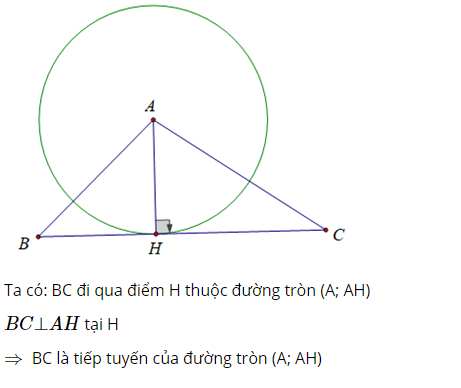
Câu 2 :
Cho đường thẳng d , điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d . Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A
.Lời giải:

Xem thêm :
Vị trí tương đối của đường thẳng và đường tròn
Định lý liên hệ giữa dây và khoảng cách từ tâm đến dây
So sánh độ dài và mối quan hệ đường kính và dây của đường tròn
Sự xác định đường tròn, tính chất đối xứng của đường tròn
.