Thừa số nguyên tố là gì? Toán đại số ở chương trình THCS bao gồm rất nhiều lý thuyết và bài tập khá mới lạ, Số nguyên tố cũng là một trong những nội dung bài học quan trọng. Số nguyên tố là gì? Thừa số nguyên tố là gì? Các bước phân tích một số ra thừa số nguyên tố, nắm được chắc phần lý thuyết chúng ta cùng nhau đi giải quyết các bài tập liên quan được dễ dàng hơn. Cùng theo dõi bài viết dưới đây để hiểu hơn về thừa số nguyên tố nha.
Định nghĩa về thừa số nguyên tố
Thừa số nguyên tố là thừa số, nhưng lại là các số nguyên tố, số nguyên tố là các số tự nhiên lớn hơn 1, là tích của 2 thừa số là số 1 và chính nó.
Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
– Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.
Lưu ý: Dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính nó.
Ví dụ:
Phân tích số 140 ra thừa số nguyên tố như sau: 140=22.5.7
Tìm hiểu thêm :
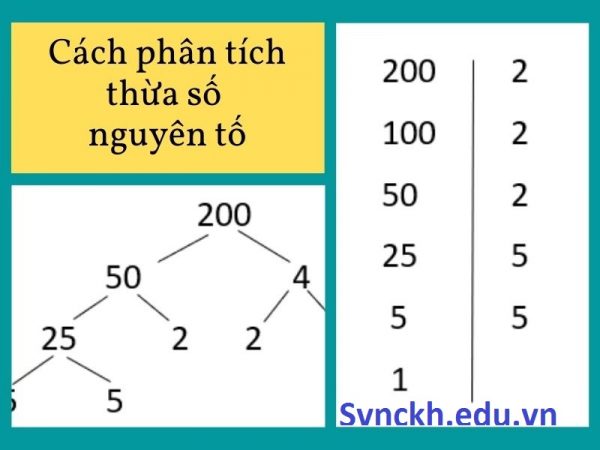
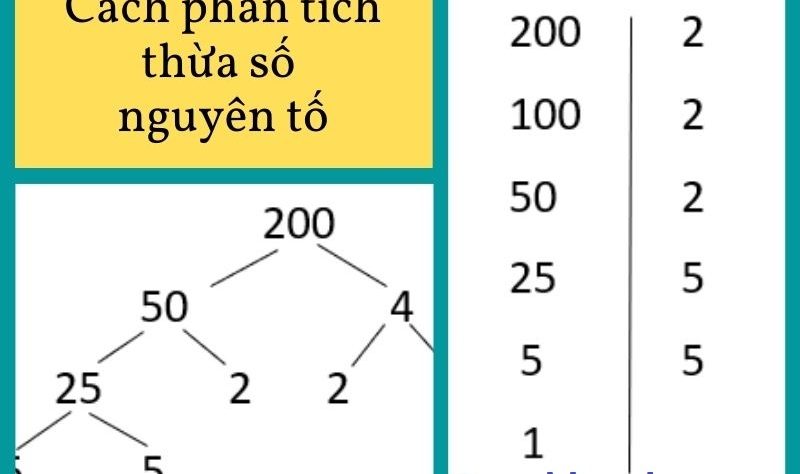
Cách phân tích một số ra thừa số nguyên tố
– Phân tích một vài một cách tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
– Muốn phân tích một vài một cách tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta khả năng làm như sau:
+ Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
+ Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
+ Tiếp tục thực hiện quy trình trên đối với b.
– Quy trình trên kéo dài cho đến khi ta được thương là một vài nguyên tố.
Lưu ý: Dù phân tích một vài một cách tự nhiên ra thừa số nguyên tố bằng cách nào thì cũng được cùng một kết quả.
– Phương pháp giải
Cách 1: Phân tích theo cột dọc
Chia số n cho một vài nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một vài nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
Ví dụ: Với số 160 ta phân tích như sau:
Như vậy: 160 = 2 . 2 . 2 . 2 . 2 . 5 = 2^5 . 5.
Cách 2: Phân tích theo hàng ngang
Viết n dưới dạng một tích các thừa số, mỗi thừa số lại viết thành tích cho đến khi các thừa số đều là số nguyên tố.
Một số dạng toán thường gặp về thừa số nguyên tố
Dạng 1: Phân tích các số cho trước ra thừa số nguyên tố
Phương pháp: Ta thường phân tích một số tự nhiên n( n > 1 ) ra thừa số nguyên tố bằng cách phân tích theo hàng dọc.
Dạng 2: Ứng dụng phân tích một số ra thừa số nguyên tố để tìm các ước của số đó.
Phương pháp
+ Phân tích số cho trước ra thừa số nguyên tố.
+ Chú ý rằng nếu c = a.b thì a và b là hai ước của c.
a=b.qa=b.q⇔a⋮b⇔a∈B(b)⇔a⋮b⇔a∈B(b) và b∈b∈Ư(a)(a) (a,b,q∈N,b≠0)
Dạng 3: Bài toán đưa về việc phân tích một số ra thừa số nguyên tố
Phương pháp:
Phân tích đề bài, đưa về việc tìm ước của một số cho trước bằng cách phân tích số đó ra thừa số nguyên tố.
Bài tập
Bài 1 : Phân tích số 420 ra thừa số nguyên tố.
Giải:
Ta có :
420 = 22 . 3 . 5 . 7
Bài 2 :
Phân tích các số sau ra thừa số nguyên tố:a) 60 b) 64 c) 285d) 1035 e) 400 g) 1000000.
Giải:
a) Ta có:
Vậy: 60 = 22.3.5
Tương tự ta có kết quả:
b) 64 = 26
c) 285 = 3 . 5 . 19
d) 1035 = 32 . 5 . 23
e) 400 = 24 . 52
g) 1000000 = 26 . 56
Bài 3 :
An phân tích các số 120, 306, 567 ra thừa số nguyên tố như sau:
120 = 2 . 3 . 4 . 5
306 = 2 . 3 . 51
567 = 92 . 7
An làm như trên có đúng không ? Hãy sửa lại trong trường hợp An làm không đúng.
Giải:
An làm không đúng vì các kết quả trên chưa phân tích hết ra thừa số nguyên tố. Chẳng hạn các số 4, 51, 9 không phải là các số nguyên tố.
Kết quả đúng phải là:
120 =23 . 3 . 5
306 = 2 . 32 . 17
567 = 34 . 7