Ở chương 1 toán lớp 9 chúng ta đã cùng nhau đi tìm hiểu về căn bậc 2 và căn bậc 3 của một số. Sang chương 2 này chúng ta sẽ cùng nhau đi tìm hiểu về hàm số bậc nhất, chương này bao gồm cả đồ thị của hàm số y=ax+b ( a # 0 ), vậy đồ thị được biểu diễn như thế nào thì chúng ta cùng nhau đi tìm hiểu nhé.
Lý thuyết đồ thị của hàm số y = ax + b ( a # 0 ) :
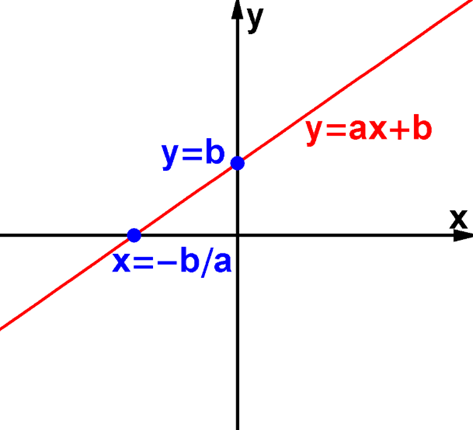
Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:
+ Cắt trục tung tại điểm có tung độ bằng b.
+ Song song với đường thẳng y = ax nếu b ≠ 0, và trùng với đường thẳng y = ax nếu b = 0
Đồ thị này cũng được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.
Chú ý: Đồ thị hàm số y = ax + b (a ≠ 0) cắt trục hoành tại điểm Q(-b/a; 0).
Ví dụ :
Gọi A là giao điểm của hai đường thẳng y = x + 1 và y = 2x + 1, tìm tọa độ của điểm A?
Giải:
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
x + 1 = 2x + 1 ⇒ x – 2x = 1 – 1
⇒ -x = 0 ⇒ x = 0
Với x = 0 thì y = 0 + 1 = 1
Suy ra, tọa độ điểm A(0; 1)
Khái niệm căn bậc 3, tính chất và biểu thức của căn bậc 3
Rút gọn biểu thức lớp 9 căn thức bậc 2 và bài tập vận dụng
Biến đổi đơn giản biểu thức chứa căn thức bậc 2
Cách vẽ đồ thị hàm số y=ax + b ( a # 0 ) :
+ Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.
Cho y = 0 thì x = -b/a ta được điểm Q(-b/a; 0) thuộc trục hoành Ox
+ Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).
+ Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.
Do đó trong trường hợp giá trị (-b/a; 0) khó xác định trên trục Ox thì ta có thể thay thế điểm Q bằng cách chọn một giá trị x1 sao cho Q(x1; y1) trong đó y1 = ax1 + b dễ xác định hơn trên mặt phẳng tọa độ.

Các dạng toán cơ bản :



Bài tập :
Bài 1 :Cho đường thẳng d xác định bởi y = 2x + 11 . Đường thẳng d’ đối xứng với đường thẳng d qua trục hoành. Vậy phương trình đường thẳng d’ là?
lời giải :
Điểm đối xứng với điểm (x, y) qua trục hoành là điểm (x; -y)
Xét đường thẳng y = 2x + 11 , thay y bởi -y ta được: -y = 2x + 11 hay y = -2x – 11
Vậy đường thẳng (d’): y = -2x – 11
Bài 2 :
Cho đường thẳng d có phương trình y = mx + m – 1 (m là tham số). Chứng minh rằng đường thẳng đã cho luôn đi qua một điểm cố định với mọi giá trị của m
lời giải :

Mục lục :
Các căn thức bậc 2 và các tính chất
Căn bậc 2 của 1 số và tính chất đầy đủ nhất