Trong mỗi dạng bài tập từ cơ bản đến nâng cao khi giải bài tập thì việc đầu tiên chúng ta phải nắm rõ được lý thuyết và công thức của dạng đó. Ở bài 3 của hình học lớp 9 này cũng thế, chúng ta sẽ cùng nhau đi tìm hiểu về Định lý liên hệ giữa dây và khoảng cách từ tâm đến dây như thế nào, để từ đó các em có kiến thức cơ bản để giải các bài tập.
Các định lí liên hệ giữa dây và khoảng cách từ tâm đến dây
Định lí 1 :
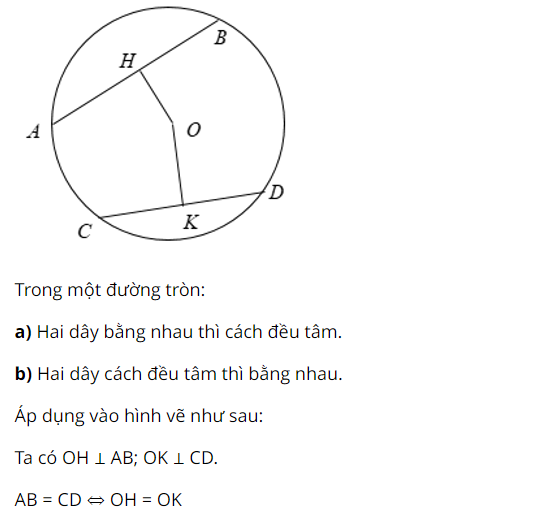
Định lí 2 :
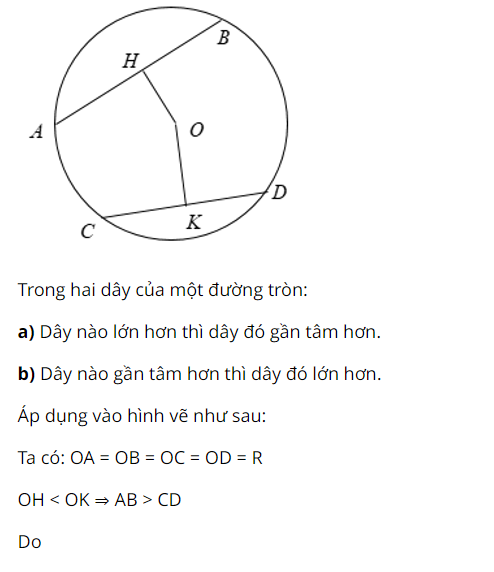
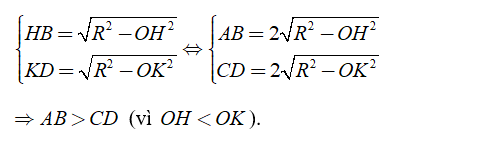
Đường thẳng song song và đường thẳng cắt nhau
Đồ thị hàm số y = ax + b ( a # 0 ) là gì? Bài tập vận dụng
Khái niệm căn bậc 3, tính chất và biểu thức của căn bậc 3
Ví dụ cụ thể
Câu 1: Cho đường tròn tâm O có bán kính là 5cm, dây AB dài 8cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD qua I vuông góc với AB. Chứng minh rằng CD = AB
Hướng dẫn:
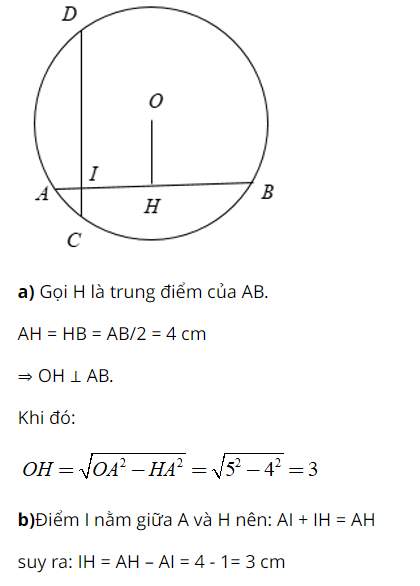

Các dạng bài toán thường gặp :
Dạng 1: Tính toán độ dài của đoạn thẳng và những yếu tố liên quan.
Cách thức giải:
Một trong những dạng toán quan trọng trong bài giảng này là tính toán độ dài của đoạn thẳng và những yếu tố liên quan giữa dây cũng như khoảng cách từ tâm đến dây. Để giải được dạng toán này, thông thường sẽ sử dụng những kiến thức cơ bản sau.
Quan hệ vuông góc của đường kính và dây:
Nếu đường kính mà vuông góc với 1 dây trong 1 đường tròn thì đi qua trung điểm của dây đó.
Nếu đường kính mà đi qua trung điểm của 1 dây và không đi qua tâm trong 1 đường tròn thì vuông góc với dây đó.
Áp dụng định lý Pitago về hệ thức lượng của tam giác vuông:
Cho tam giác ΔABC vuông tại A. Ta có: AB² + AC² = BC²
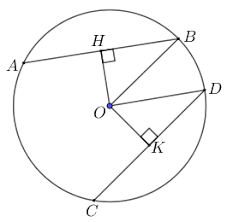
Dạng 2: So sánh giữa hai đoạn thẳng
Cách thức giải:
Đối với bài giảng về dạng kiến thức này, so sánh giữa hai đoạn thẳng là một trong những dạng toán cơ bản, đặc biệt là thường bắt gặp trong những bài kiểm tra. Thông thường đối với dạng toán này, để có thể giải cần áp dụng những kiến thức cơ bản sau:
Đối với 1 đường tròn:
2 dây bằng nhau thì sẽ cách đều tâm.
2 dây cách đều với tâm thì sẽ bằng nhau.
Trong 1 đường tròn, 2 dây của đường tròn sẽ:
Dây nào có độ dài lớn hơn thì dây đó sẽ gần tâm hơn.
Dây nào gần với tâm hơn thì dây đó sẽ lớn hơn.
Chứng minh 2 tam giác bằng nhau và áp dụng quan hệ giữa những yếu tố trong tam giác như: Trường hợp cạnh – cạnh – cạnh, trường hợp cạnh – góc – cạnh, hay trường hợp góc – cạnh – góc.
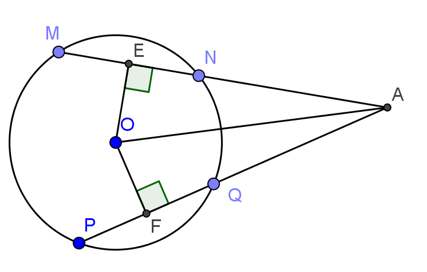
Bài tập vận dụng :
Câu 1: Cho đường tròn tâm O bán kính là 5, dây AB = 8
a) Tính khoảng cách từ O đến AB
b) Gọi I là điểm thuộc dây AB sao cho AI = 1 , kẻ dây CD đi qua I vuông góc với AB. Chứng minh rằng AB = CD
Lời giải :
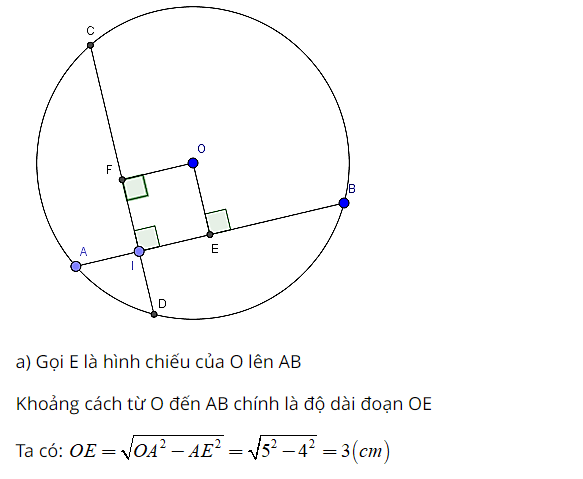
b) Gọi F là hình chiếu của O lên CD
Khi đó khoảng cách của O đến CD chính là OF
Tứ giác OFIE có ba góc vuông nên là hình chữ nhật
Do đó: OF = EI = AE – AI = 4 – 1 = 3
Suy ra OE = OF theo định lí 1 nên AB = CD
Câu 2:
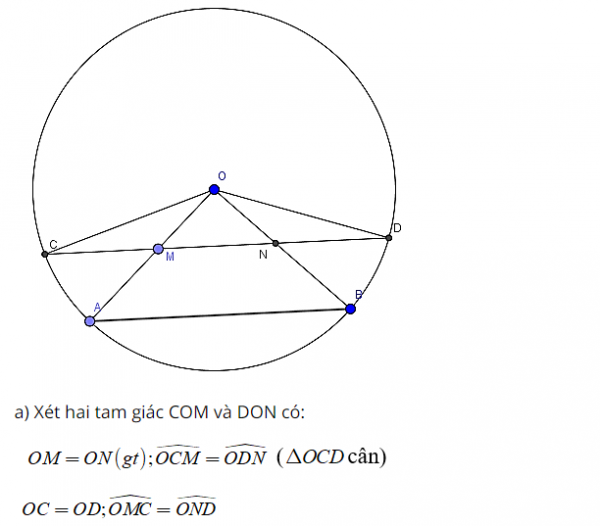
Cho đường tròn (O; R) . Lấy các điểm A và B trên đường tròn. Trên bán kính OA, OB lấy các điểm M, N sao cho OM = ON . Vẽ dây CD đi qua MN; M giữa C và N
a) Chứng minh: CM = DN
b) Giả sử Tam giác AOB 90 độ. Tính OM theo R sao cho CM = MN = ND
Lời giải :

Xem thêm :
So sánh độ dài và mối quan hệ đường kính và dây của đường tròn
Sự xác định đường tròn, tính chất đối xứng của đường tròn
Bảng lượng giác là gì? Cấu tạo của bảng lượng giác
Các hình thức về cạnh và đường cao trong tam giác vuông