Môn toán lớp 9 có rất nhiều các dạng bài toán khó khác nhau, Đường kính và dây của đường tròn cũng nằm trong số đó, vậy làm thế nào để hiểu được lý thuyết và nắm được công thức để giải những dạng bài tập từ cơ bản đến nâng cao. Chính vì vậy ở bài viết dưới đây chúng tôi sẽ tóm tắt nội dung cũng như công thức để các em học sinh có thể theo dõi và áp dụng theo.
Cung và dây cung của đường tròn:
Cho đường tròn có tâm là O và có 2 điểm phân biệt là A và B nằm trên đường tròn thì 2 điểm này sẽ chia đường tròn làm 2 phần. Đối với 2 phần này, mỗi phần sẽ được xem là một cung.
Trong đó:
2 điểm A và B được gọi là 2 mút của cung.
Đoạn thẳng nối liền 2 mút của cung được gọi là dây cung (dây).
Dây cung đi qua tâm của đường tròn được gọi là đường kính.
Ngoài ra trong một đường tròn còn có mối quan hệ giữa đường kính và dây cung như sau: Đường kính sẽ dài gấp đôi bán kính.


Sự xác định đường tròn, tính chất đối xứng của đường tròn
Bảng lượng giác là gì? Cấu tạo của bảng lượng giác
Các hình thức về cạnh và đường cao trong tam giác vuông
Lưu ý:
Trong quan hệ vuông góc giữa đường kính với dây đường tròn, nếu đường kính mà đi qua trung điểm của 1 dây thì có thể sẽ không vuông góc với đó.
Giả sử 2 đường kính của đường tròn (O , R) là AB và CD.
Khi đó ta có CD cũng là 1 dây cung của đường tròn tâm O.
Mà O ∈ CD đồng thời OC = OD (do CD là đường kính của đường tròn tâm O)
⇒ O chính là trung điểm của CD.
⇒ Khi đó, đường kính AB sẽ đi qua trung điểm O của CD nhưng đường kính sẽ không vuông góc với dây đường tròn.
Các dạng toán thường gặp
Tính độ dài đoạn thẳng và các yếu tố liên quan.
Phương pháp:
Ta thường sử dụng các kiến thức sau:
+) Quan hệ vuông góc giữa đường kính và dây
Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Dùng định lý Pytago, hệ thức lượng trong tam giác vuông.
Bài tập vận dụng :
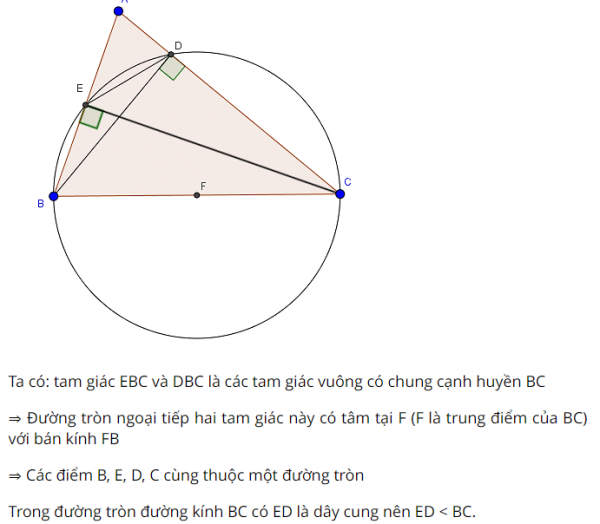
Câu 1: Cho tam giác ABC có đường cao là BD, CE. Chứng minh rằng B, D, C, E cùng một đường tròn và ED < BC .
lời giải :
câu 2 :
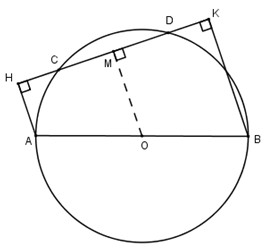
Cho đường tròn ( O) đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH=DK
lời giải:

xem thêm :
Đường thẳng song song và đường thẳng cắt nhau
Đồ thị hàm số y = ax + b ( a # 0 ) là gì? Bài tập vận dụng
Khái niệm căn bậc 3, tính chất và biểu thức của căn bậc 3
Rút gọn biểu thức lớp 9 căn thức bậc 2 và bài tập vận dụng